Question Number 110888 by mnjuly1970 last updated on 31/Aug/20
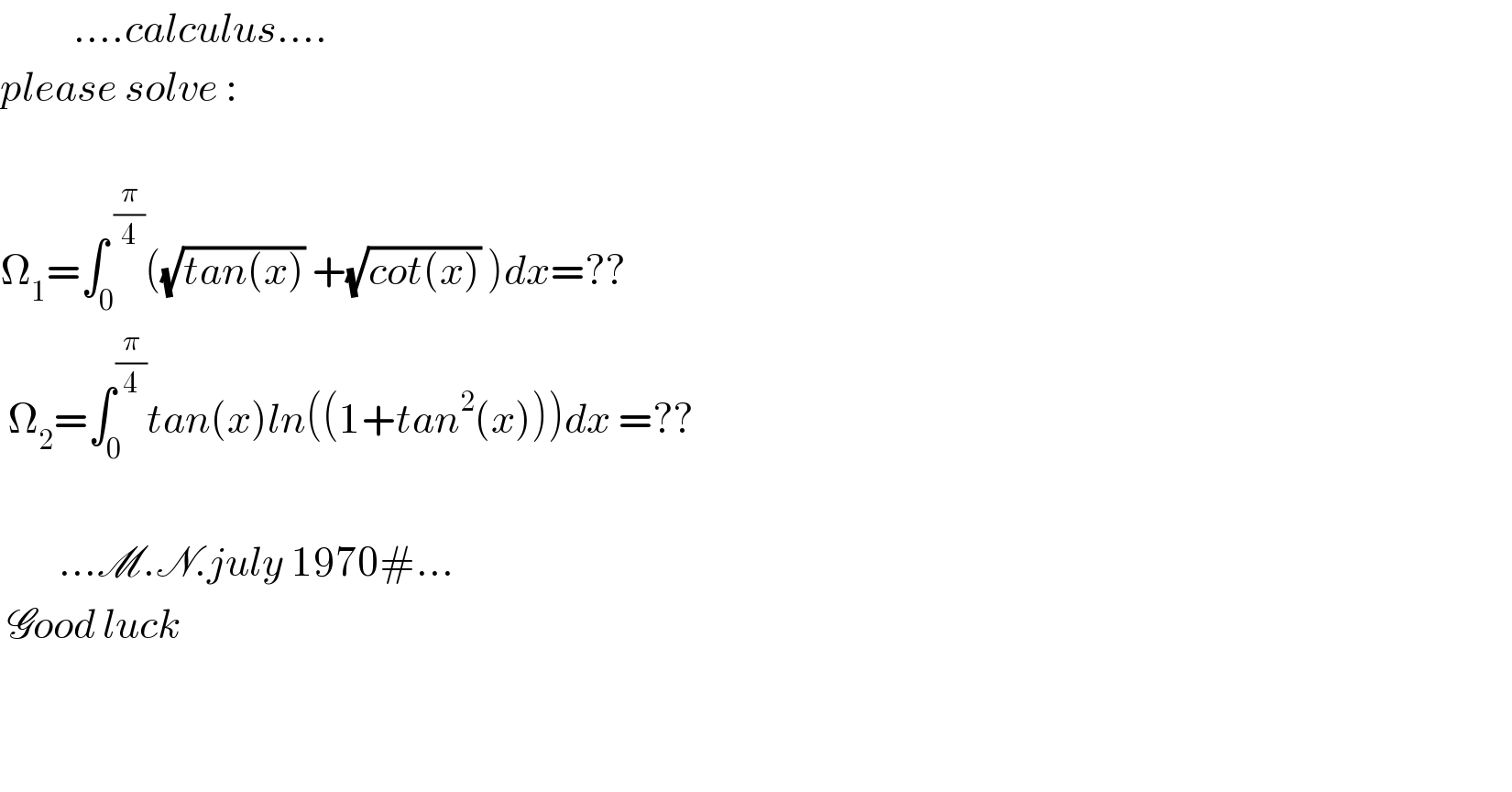
$$\:\:\:\:\:\:\:\:\:\:….{calculus}…. \\ $$$${please}\:{solve}\:: \\ $$$$ \\ $$$$\Omega_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \left(\sqrt{{tan}\left({x}\right)}\:+\sqrt{{cot}\left({x}\right)}\:\right){dx}=?? \\ $$$$\:\Omega_{\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}\left({x}\right){ln}\left(\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)\right)\right){dx}\:=?? \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:…\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}#… \\ $$$$\:\mathscr{G}{ood}\:{luck} \\ $$$$ \\ $$$$ \\ $$
Answered by bobhans last updated on 31/Aug/20

$$\mathrm{tan}\:\mathrm{x}=\mathrm{u}^{\mathrm{2}} \:\Rightarrow\mathrm{dx}\:=\:\mathrm{2u}.\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{du} \\ $$$$\mathrm{dx}=\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }\:\mathrm{du}\: \\ $$$$\int\:\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)\left(\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }\right)\mathrm{du}=\int\left(\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{u}}\right)\left(\frac{\mathrm{2u}}{\mathrm{u}^{\mathrm{4}} +\mathrm{1}}\right)\mathrm{du} \\ $$$$=\mathrm{2}\int\:\:\left(\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{u}^{\mathrm{4}} +\mathrm{1}}\right)\mathrm{du}\:=\mathrm{2}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}\:\mathrm{du} \\ $$$$=\mathrm{2}\int\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:\mathrm{du}\: \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{du}=\mathrm{2}\left\{\int\frac{\mathrm{d}\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{du}+\int\frac{\frac{\mathrm{2}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{du}\right\} \\ $$
Answered by Dwaipayan Shikari last updated on 31/Aug/20
![∫_0 ^(π/4) ((sinx+cosx)/( (√(sinxcosx))))dx=(√2)∫_0 ^(π/4) ((sinx+cosx)/( (√(1−(sinx−cosx)^2 ))))dx =(√2)∫_(−1) ^0 (dt/( (√(1−t^2 )))) =−(√2)∫_0 ^(−1) (dt/( (√(1−t^2 ))))=−(√2) [sin^(−1) t]_0 ^(−1) =(π/( (√2)))](https://www.tinkutara.com/question/Q110899.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sinx}+{cosx}}{\:\sqrt{{sinxcosx}}}{dx}=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sinx}+{cosx}}{\:\sqrt{\mathrm{1}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }}{dx} \\ $$$$=\sqrt{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$=−\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{−\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=−\sqrt{\mathrm{2}}\:\left[{sin}^{−\mathrm{1}} {t}\right]_{\mathrm{0}} ^{−\mathrm{1}} =\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mnjuly1970 last updated on 01/Sep/20
$${thank}\:{you}\:{so}\:{much}…. \\ $$
Answered by mathmax by abdo last updated on 31/Aug/20
![I =∫_0 ^(π/4) ((√(tanx))+(√(1/(tanx))))dx changement (√(tanx))=t give tanx =t^2 ⇒ I =∫_0 ^1 (t+(1/t)) ((2t)/(1+t^4 )) dt =2 ∫_0 ^1 (((t^2 +1)/t))(t/(1+t^4 ))dt =2∫_0 ^1 ((t^2 +1)/(t^4 +1)) dt =2 ∫_0 ^1 ((1+(1/t^2 ))/(t^2 +(1/t^2 ))) dt =2 ∫_0 ^1 ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt =_(t−(1/t)=u) 2 ∫_(−∞) ^0 (du/(u^2 +2)) =_(u=−z) 2∫_(+∞) ^0 ((−dz)/(z^2 +2)) =2∫_0 ^∞ (dz/(z^2 +2)) =_(z=(√2)α) 2∫_0 ^∞ (((√2) dα)/(2(1+α^2 ))) =(√2) [arctanα]_0 ^∞ =(√2)×(π/2) ⇒I =((π(√2))/2)](https://www.tinkutara.com/question/Q110937.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\sqrt{\mathrm{tanx}}+\sqrt{\frac{\mathrm{1}}{\mathrm{tanx}}}\right)\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\mathrm{tanx}}=\mathrm{t}\:\mathrm{give}\:\mathrm{tanx}\:=\mathrm{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)\:\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\:\mathrm{dt}\:\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}}\right)\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{1}}\:\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt} \\ $$$$=_{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}=\mathrm{u}} \:\:\:\mathrm{2}\:\int_{−\infty} ^{\mathrm{0}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\:=_{\mathrm{u}=−\mathrm{z}} \:\:\:\mathrm{2}\int_{+\infty} ^{\mathrm{0}} \:\frac{−\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2}}\:=_{\mathrm{z}=\sqrt{\mathrm{2}}\alpha} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{\mathrm{2}}\:\mathrm{d}\alpha}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:=\sqrt{\mathrm{2}}\:\left[\mathrm{arctan}\alpha\right]_{\mathrm{0}} ^{\infty} \:=\sqrt{\mathrm{2}}×\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{I}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
