Menu Close

calculus-prove-that-0-1-x-n-1-ln-2-1-x-dx-2-n-k-1-n-H-k-k-

Tinku Tara 0 Comments
Pin




Question Number 126631 by mnjuly1970 last updated on 23/Dec/20
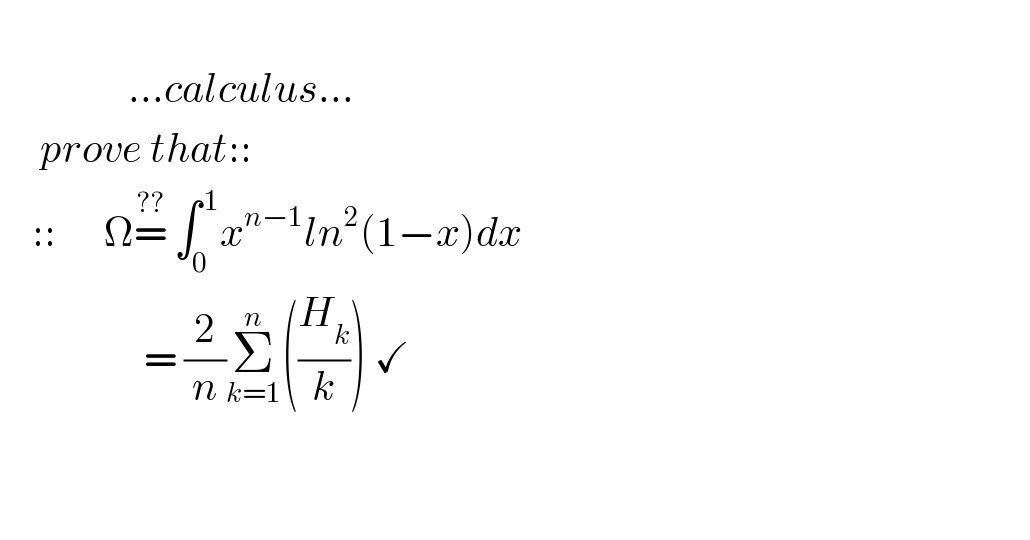
...calculus... prove that:: :: Ω=^(??) ∫_0 ^( 1) x^(n−1) ln^2 (1−x)dx = (2/n)Σ_(k=1) ^n ((H_k /k)) ✓
$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{calculus}… \\ $$$$\:\:\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:::\:\:\:\:\:\:\Omega\overset{??} {=}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{H}_{{k}} }{{k}}\right)\:\checkmark \\ $$$$ \\ $$$$\:\:\: \\ $$
Answered by mindispower last updated on 23/Dec/20
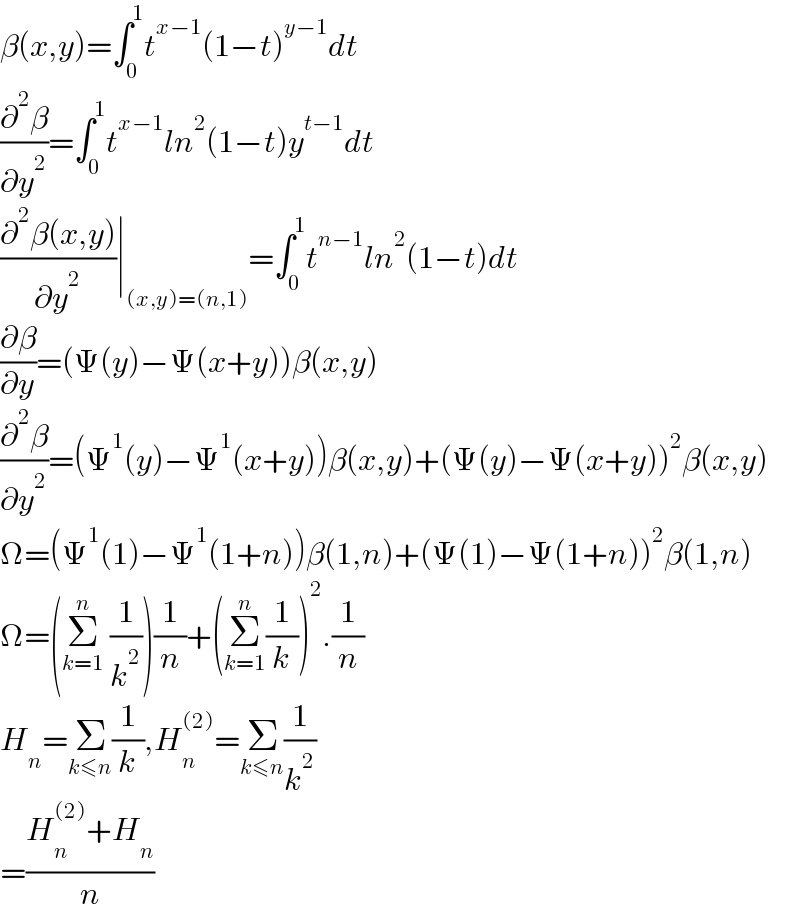
β(x,y)=∫_0 ^1 t^(x−1) (1−t)^(y−1) dt (∂^2 β/∂y^2 )=∫_0 ^1 t^(x−1) ln^2 (1−t)y^(t−1) dt ((∂^2 β(x,y))/∂y^2 )∣_((x,y)=(n,1)) =∫_0 ^1 t^(n−1) ln^2 (1−t)dt (∂β/∂y)=(Ψ(y)−Ψ(x+y))β(x,y) (∂^2 β/∂y^2 )=(Ψ^1 (y)−Ψ^1 (x+y))β(x,y)+(Ψ(y)−Ψ(x+y))^2 β(x,y) Ω=(Ψ^1 (1)−Ψ^1 (1+n))β(1,n)+(Ψ(1)−Ψ(1+n))^2 β(1,n) Ω=(Σ_(k=1) ^n (1/k^2 ))(1/n)+(Σ_(k=1) ^n (1/k))^2 .(1/n) H_n =Σ_(k≤n) (1/k),H_n ^((2)) =Σ_(k≤n) (1/k^2 ) =((H_n ^((2)) +H_n )/n)
$$\beta\left({x},{y}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{x}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{y}−\mathrm{1}} {dt} \\ $$$$\frac{\partial^{\mathrm{2}} \beta}{\partial{y}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{x}−\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{t}\right){y}^{{t}−\mathrm{1}} {dt} \\ $$$$\frac{\partial^{\mathrm{2}} \beta\left({x},{y}\right)}{\partial{y}^{\mathrm{2}} }\mid_{\left({x},{y}\right)=\left({n},\mathrm{1}\right)} =\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{t}\right){dt} \\ $$$$\frac{\partial\beta}{\partial{y}}=\left(\Psi\left({y}\right)−\Psi\left({x}+{y}\right)\right)\beta\left({x},{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} \beta}{\partial{y}^{\mathrm{2}} }=\left(\Psi^{\mathrm{1}} \left({y}\right)−\Psi^{\mathrm{1}} \left({x}+{y}\right)\right)\beta\left({x},{y}\right)+\left(\Psi\left({y}\right)−\Psi\left({x}+{y}\right)\right)^{\mathrm{2}} \beta\left({x},{y}\right) \\ $$$$\Omega=\left(\Psi^{\mathrm{1}} \left(\mathrm{1}\right)−\Psi^{\mathrm{1}} \left(\mathrm{1}+{n}\right)\right)\beta\left(\mathrm{1},{n}\right)+\left(\Psi\left(\mathrm{1}\right)−\Psi\left(\mathrm{1}+{n}\right)\right)^{\mathrm{2}} \beta\left(\mathrm{1},{n}\right) \\ $$$$\Omega=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)\frac{\mathrm{1}}{{n}}+\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} .\frac{\mathrm{1}}{{n}} \\ $$$${H}_{{n}} =\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{k}},{H}_{{n}} ^{\left(\mathrm{2}\right)} =\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$=\frac{{H}_{{n}} ^{\left(\mathrm{2}\right)} +{H}_{{n}} }{{n}} \\ $$
Commented by mnjuly1970 last updated on 23/Dec/20
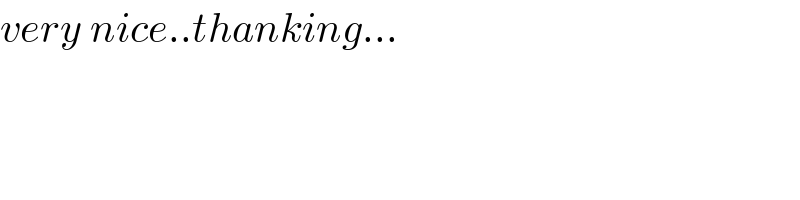
very nice..thanking...
$${very}\:{nice}..{thanking}… \\ $$
Answered by mnjuly1970 last updated on 23/Dec/20
solution: consider: I_n =∫_0 ^( 1) x^(n−1) ln(1−x)dx we can write: I_n =(1/n)∫(x^n −1) ^′ ln(1−x)dx =(1/n){[(x^n −1)ln(1−x)]_0 ^1 +∫_0 ^( 1) ((x^n −1)/(1−x))dx} =((−H_n )/n) .... (1) put:: Ω=∫_0 ^( 1) x^(n−1) ln^2 (1−x)dx =(1/n)∫_0 ^( 1) (x^n −1) ^′ ln^2 (1−x)dx =(1/n){[(x^n −1)ln^2 (1−x)]_0 ^1 +2∫_0 ^( 1) ((x^n −1)/(1−x))ln(1−x)dx =(2/n) ∫_0 ^( 1) (−Σ_(k=1) ^n x^(k−1) )ln(1−x)dx =((−2)/n^2 )Σ_(k=1) ^n ∫_0 ^( 1) x^(k−1) ln(1−x)dx=(2/n)Σ_(k=1) ^n (H_k /k) ✓
$${solution}: \\ $$$$\:\:{consider}: \\ $$$$\:\:\:\:\:{I}_{{n}} =\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:{we}\:{can}\:{write}: \\ $$$$\:\:\:\:\:{I}_{{n}} =\frac{\mathrm{1}}{{n}}\int\left({x}^{{n}} −\mathrm{1}\right)\overset{'} {\:}{ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\left\{\left[\left({x}^{{n}} −\mathrm{1}\right){ln}\left(\mathrm{1}−{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}} −\mathrm{1}}{\mathrm{1}−{x}}{dx}\right\} \\ $$$$=\frac{−{H}_{{n}} }{{n}}\:\:….\:\left(\mathrm{1}\right) \\ $$$$\:{put}::\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({x}^{{n}} −\mathrm{1}\right)\overset{'} {\:}{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\left\{\left[\left({x}^{{n}} −\mathrm{1}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}} −\mathrm{1}}{\mathrm{1}−{x}}{ln}\left(\mathrm{1}−{x}\right){dx}\right. \\ $$$$\:\:=\frac{\mathrm{2}}{{n}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}^{{k}−\mathrm{1}} \right){ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:=\frac{−\mathrm{2}}{{n}^{\mathrm{2}} }\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{k}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}=\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{H}_{{k}} }{{k}}\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *