Question Number 112119 by mnjuly1970 last updated on 06/Sep/20
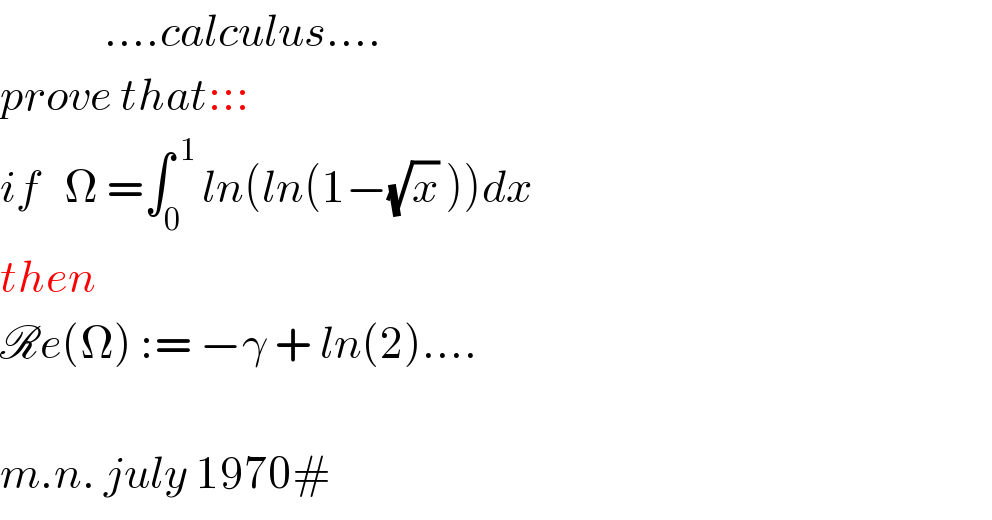
$$\:\:\:\:\:\:\:\:\:\:\:\:\:….{calculus}…. \\ $$$${prove}\:{that}::: \\ $$$${if}\:\:\:\Omega\:=\int_{\mathrm{0}\:\:} ^{\:\mathrm{1}} {ln}\left({ln}\left(\mathrm{1}−\sqrt{{x}}\:\right)\right){dx} \\ $$$${then} \\ $$$$\mathscr{R}{e}\left(\Omega\right)\::=\:−\gamma\:+\:{ln}\left(\mathrm{2}\right)…. \\ $$$$ \\ $$$${m}.{n}.\:{july}\:\mathrm{1970}# \\ $$
Answered by maths mind last updated on 06/Sep/20
![u=ln(1−(√x))⇒x=(1−e^u )^2 ⇒dx=−2e^u (1−e^u )du Ω=∫_0 ^(−∞) ln(u).−2e^u (1−e^u )du we use ln(z)=ln∣z∣+iarg(z) z∉IR_− ^∗ put u=−t⇒=∫_0 ^∞ ln(−t).2e^(−t) (1−e^(−t) )dt =∫_0 ^∞ (ln(t)+iπ)2e^t (1−e^t )dt Re(Ω)=∫_0 ^∞ 2ln(t)e^(−t) dt−2∫_0 ^∞ ln(t)e^(−2t) dt Γ(z)=∫_0 ^∞ t^(z−1) e^(−t) dt⇒Γ′(1)=∫_0 ^(+∞) ln(t)e^(−t) dt=γ Re(Ω)=−2γ−2∫_0 ^(+∞) ln((s/2))e^(−s) .(ds/2) =−2γ−∫_0 ^(+∞) ln(s)e^(−s) ds+ln(2)∫_0 ^(+∞) e^(−s) ds =−2γ+γ+ln(2)[−e^(−s) ]_0 ^(+∞) =−γ+ln(2)](https://www.tinkutara.com/question/Q112178.png)
$${u}={ln}\left(\mathrm{1}−\sqrt{{x}}\right)\Rightarrow{x}=\left(\mathrm{1}−{e}^{{u}} \right)^{\mathrm{2}} \Rightarrow{dx}=−\mathrm{2}{e}^{{u}} \left(\mathrm{1}−{e}^{{u}} \right){du} \\ $$$$\Omega=\int_{\mathrm{0}} ^{−\infty} {ln}\left({u}\right).−\mathrm{2}{e}^{{u}} \left(\mathrm{1}−{e}^{{u}} \right){du} \\ $$$${we}\:{use}\:{ln}\left({z}\right)={ln}\mid{z}\mid+{iarg}\left({z}\right)\:{z}\notin{IR}_{−} ^{\ast} \\ $$$${put}\:{u}=−{t}\Rightarrow=\int_{\mathrm{0}} ^{\infty} {ln}\left(−{t}\right).\mathrm{2}{e}^{−{t}} \left(\mathrm{1}−{e}^{−{t}} \right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left({ln}\left({t}\right)+{i}\pi\right)\mathrm{2}{e}^{{t}} \left(\mathrm{1}−{e}^{{t}} \right){dt} \\ $$$${Re}\left(\Omega\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{2}{ln}\left({t}\right){e}^{−{t}} {dt}−\mathrm{2}\int_{\mathrm{0}} ^{\infty} {ln}\left({t}\right){e}^{−\mathrm{2}{t}} {dt} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{z}−\mathrm{1}} {e}^{−{t}} {dt}\Rightarrow\Gamma'\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{+\infty} {ln}\left({t}\right){e}^{−{t}} {dt}=\gamma \\ $$$${Re}\left(\Omega\right)=−\mathrm{2}\gamma−\mathrm{2}\int_{\mathrm{0}} ^{+\infty} {ln}\left(\frac{{s}}{\mathrm{2}}\right){e}^{−{s}} .\frac{{ds}}{\mathrm{2}} \\ $$$$=−\mathrm{2}\gamma−\int_{\mathrm{0}} ^{+\infty} {ln}\left({s}\right){e}^{−{s}} {ds}+{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{+\infty} {e}^{−{s}} {ds} \\ $$$$=−\mathrm{2}\gamma+\gamma+{ln}\left(\mathrm{2}\right)\left[−{e}^{−{s}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=−\gamma+{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 06/Sep/20

$${peace}\:{be}\:{upon}\:{you}\:{master}\: \\ $$$$..{gratful}\:{for}\:{your}\:{attantion} \\ $$$${and}\:{favor}… \\ $$
