Question Number 118023 by 1549442205PVT last updated on 14/Oct/20
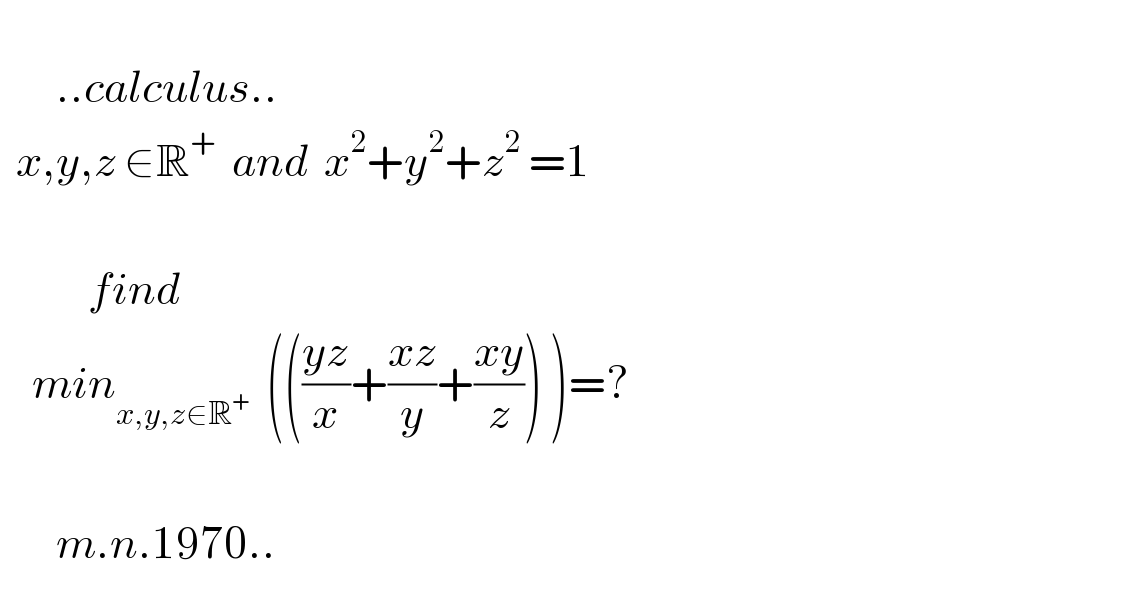
$$ \\ $$$$\:\:\:\:\:\:\:..{calculus}.. \\ $$$$\:\:{x},{y},{z}\:\in\mathbb{R}^{+} \:\:{and}\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:=\mathrm{1} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{find}\:\:\:\:\:\: \\ $$$$\:\:\:\:{min}_{{x},{y},{z}\in\mathbb{R}^{+\:\:\:\:} } \left(\left(\frac{{yz}}{{x}}+\frac{{xz}}{{y}}+\frac{{xy}}{{z}}\right)\:\right)=? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970}.. \\ $$
Answered by MJS_new last updated on 14/Oct/20
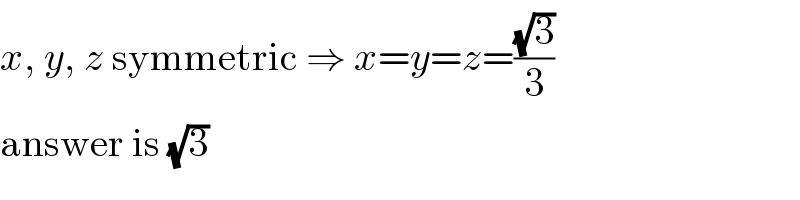
$${x},\:{y},\:{z}\:\mathrm{symmetric}\:\Rightarrow\:{x}={y}={z}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{3}} \\ $$
