Question Number 146164 by mnjuly1970 last updated on 11/Jul/21
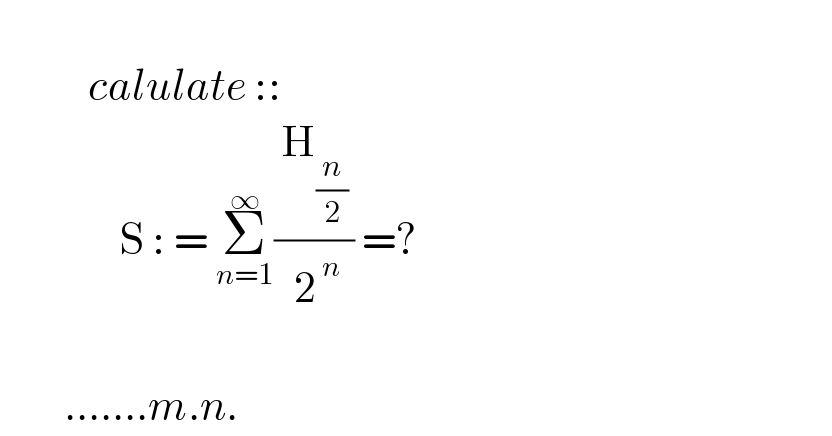
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{calulate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{S}\::\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\mathrm{H}_{\frac{{n}}{\mathrm{2}}\:} }{\:\mathrm{2}^{\:{n}} }\:=? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:…….{m}.{n}. \\ $$
Answered by qaz last updated on 12/Jul/21
![Σ_(n=1) ^∞ (1/2^n )∫_0 ^1 ((1−x^(n/2) )/(1−x))dx =∫_0 ^1 (1/(1−x))Σ_(n=1) ^∞ [(1/2^n )−(((√x)/2))^n ]dx =∫_0 ^1 (1/(1−x))(1−(((√x)/2)/(1−((√x)/2))))dx =2∫_0 ^1 (dx/((1+(√x))(2−(√x)))) =4∫_0 ^1 ((xdx)/((1+x)(2−x))) =(4/3)∫_0 ^1 ((2/(2−x))−(1/(1+x)))dx =(4/3){−2ln(2−x)−ln(1+x)}_0 ^1 =(4/3)ln2](https://www.tinkutara.com/question/Q146222.png)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{x}^{\mathrm{n}/\mathrm{2}} }{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }−\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)^{\mathrm{n}} \right]\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\left(\mathrm{1}−\frac{\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{1}−\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\left(\mathrm{1}+\sqrt{\mathrm{x}}\right)\left(\mathrm{2}−\sqrt{\mathrm{x}}\right)} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xdx}}{\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{2}−\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{2}−\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left\{−\mathrm{2ln}\left(\mathrm{2}−\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\mathrm{ln2} \\ $$
Commented by mnjuly1970 last updated on 12/Jul/21

$$\:\:{thx}\:{mr}\:{qaz}…{nice}\:{solution}… \\ $$
