calulate-using-Riemann-sums-tbe-limit-of-this-sequence-k-n-2n-sin-pi-k-

Question Number 100297 by Coronavirus last updated on 26/Jun/20

c a l u l a t e u s i n g R i e m a n n s u m s

t b e l i m i t o f t h i s s e q u e n c e

\underset{k = n}{\sum^{2 n}} \sin (\frac{π}{k})

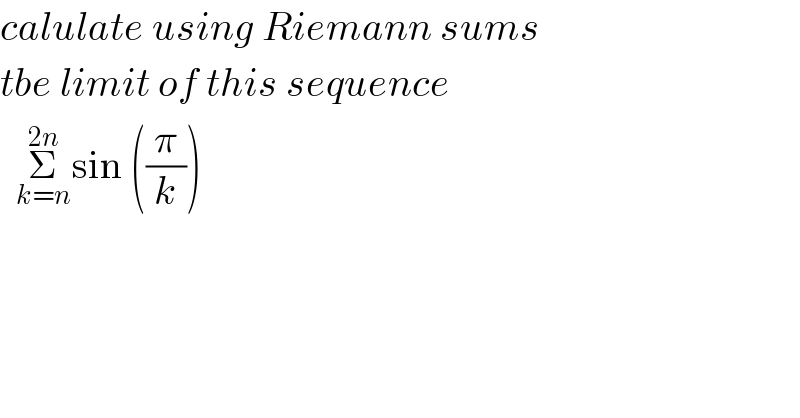
Answered by abdomsup last updated on 26/Jun/20

A_{n} =_{p = k - n} \sum_{p = 0}^{n} s i n (\frac{π}{p + n})

w e h a v e x - \frac{x^{3}}{6} ⩽ s i n x ⩽ x \Rightarrow

\frac{π}{k} - \frac{π^{3}}{6 k^{3}} ⩽ s i n (\frac{π}{k}) ⩽ \frac{π}{k}

\Rightarrow \sum_{k = n}^{2 n} \frac{π}{k} - π^{3} \sum_{k = n}^{2 n} \frac{1}{k^{3}}

⩽ \sum_{k = n}^{2 n} s i n (\frac{π}{k}) ⩽ π \sum_{k = n}^{2 n} \frac{1}{k}

π \sum_{p = 0}^{n} \frac{1}{p + n} - π^{3} \sum_{p = 0}^{n} \frac{1}{{(p + n)}^{3}}

⩽ \sum_{k = n}^{2 n} s i n (\frac{π}{k}) ⩽ π \sum_{p = 0}^{n} \frac{1}{p + n}

w e h a v e \sum_{p = 0}^{n} \frac{1}{p + n}

\frac{1}{n} + \frac{1}{n + 1} + \dots . + \frac{1}{2 n}

1 + \frac{1}{n} + \dots . + \frac{1}{n - 1} + \dots . + \frac{1}{2 n}

- H_{n - 1} = H_{2 n} - H_{n - 1}

= l n (2 n) + γ + 0 (\frac{1}{2 n}) - l n (n - 1)

- γ - o (\frac{1}{n - 1}) \to l n 2

i t s c l e a r t h a t \sum_{p = 0}^{n} \frac{1}{{(p + n)}^{3}} \to 0

b e c a u s e Σ) \dots) ⩽ \sum_{0}^{n} \frac{1}{n^{3}} = \frac{n + 1}{n^{3}}

\Rightarrow {l i m}_{n \to + \infty} \sum_{k = n}^{2 n} s i n (\frac{k}{n}) = π l n 2

Commented by Coronavirus last updated on 26/Jun/20

Thanks you Mr

Commented by DGmichael last updated on 26/Jun/20

��

Commented by mathmax by abdo last updated on 26/Jun/20

you are welcome sir

Commented by Ar Brandon last updated on 26/Jun/20

Qui a compris ? ��

Commented by Ar Brandon last updated on 26/Jun/20

Sir is H_{n} a special function ?

Commented by mathmax by abdo last updated on 26/Jun/20

H_{n} = 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} is harmonic sequence

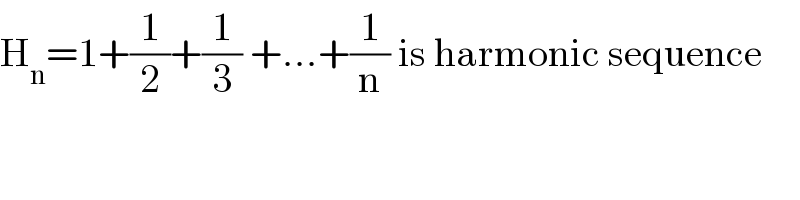
Commented by Ar Brandon last updated on 27/Jun/20

OK thank you Sir