Can-anyone-find-any-error-in-my-attempt-to-improve-upon-the-Cardano-s-cubic-formula-or-as-an-alternate-to-the-trigonometric-solution-here-it-goes-X-3-pX-q-0-let-X-p-x-and-with

FacebookTweetPin

Question Number 128007 by ajfour last updated on 03/Jan/21

$$Cananyonefindanyerrorin$$$$myattempttoimproveupon$$$$the{Cardano}^{\prime }scubicformula..$$$$orasanalternatetothe$$$$trigonometricsolution\dots$$$$hereitgoes:$$$$X^3-pX-q=0$$$$let\frac{X}{\sqrt{p}}=x;andwith\frac{q}{p\sqrt{p}}=c,$$$$x^3-x-c=0$$$$let\mathit{x}=(\mathit{k}+1)(\mathit{p}+\mathit{q})$$$$=(\mathit{p}+\mathit{k}\mathit{q})+(\mathit{k}\mathit{p}+\mathit{q})$$$$p^3+k^3{q}^3+3kpq(p+kq)+$$$$k^3{p}^3+q^3+3kpq(kp+q)$$$$-(p+kq)-(kp+q)=c$$$$\Rightarrow$$$$(1+k^3)(p^3+q^3)+$$$$(p+kq)(3kpq-1)+$$$$(kp+q)(3kpq-1)=c$$$$let3\mathit{k}\mathit{p}\mathit{q}=1\Rightarrow$$$$p^3+q^3=\frac{c}{1+k^3}$$$$\mathrm{\&}{p}^3{q}^3=\frac{1}{27k^3};hence$$$$p^3,q^3=$$$$\frac{c}{2(1+k^3)}\pm \sqrt{\frac{c^2}{4{(1+k^3)}^2}-\frac{1}{27k^3}}$$$$letschooseuponavalueof\mathit{k}$$$$suchthatD=0$$$$\Rightarrow 4{(1+k^3)}^2=27c^2{k}^3\dots ..\left(I\right)$$$$(justaquadratic..)$$$$firstfor{c}^2>\frac{8}{27}wealwayscan$$$$gettworealkvalues,andeven$$$$p=qthen.$$$$x=(k+1)(p+q)$$$$=2(k+1)p$$$$x=2(k+1){\left[\frac{c}{2(1+k^3)}\right]}^{1/3}$$$$butsimplypq=\frac{1}{3k}hence$$$$x=2(k+1)p=\frac{2(k+1)}{\sqrt{3k}}.$$$$\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}$$$$evenforc=1idintgeta$$$$correctanswer,pleasehelp$$$$error-freeingit.(\mathcal{T}hanks!)$$

Commented by MJS_new last updated on 04/Jan/21

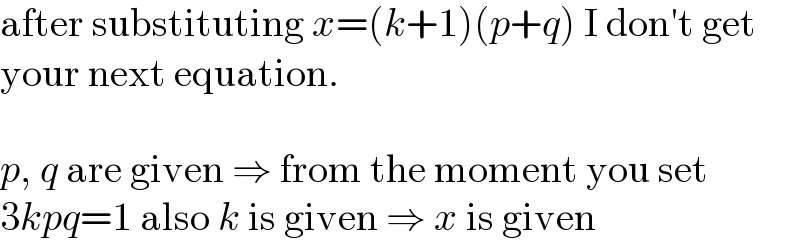
$$\mathrm{after}\mathrm{substituting}x=(k+1)(p+q)\mathrm{I}{\mathrm{don}}^{\prime }\mathrm{t}\mathrm{get}$$$$\mathrm{your}\mathrm{next}\mathrm{equation}.$$$$$$$$p,q\mathrm{are}\mathrm{given}\Rightarrow \mathrm{from}\mathrm{the}\mathrm{moment}\mathrm{you}\mathrm{set}$$$$3kpq=1\mathrm{also}k\mathrm{is}\mathrm{given}\Rightarrow x\mathrm{is}\mathrm{given}$$

Commented by ajfour last updated on 04/Jan/21

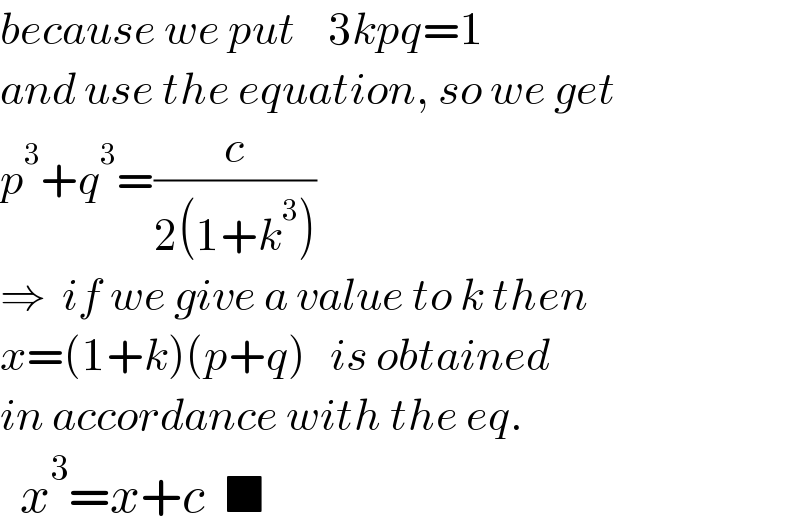
$$becauseweput3kpq=1$$$$andusetheequation,soweget$$$$p^3+q^3=\frac{c}{2(1+k^3)}$$$$\Rightarrow ifwegiveavaluetokthen$$$$x=(1+k)(p+q)isobtained$$$$inaccordancewiththeeq.$$$$x^3=x+c\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/15.0.3/svg/25fc.svg">}$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin