Menu Close

Can-anyone-please-resolve-the-Q-159787-in-details-

Tinku Tara 0 Comments
Pin




Question Number 159973 by abdullah_ff last updated on 23/Nov/21
Can anyone please resolve the Q 159787 in details..
$${Can}\:{anyone}\:{please}\:{resolve}\:{the} \\ $$$${Q}\:\mathrm{159787}\:{in}\:{details}.. \\ $$
Commented by tounghoungko last updated on 23/Nov/21
your question had solved by cortano sir. why you ask again?
$${your}\:{question}\:{had}\:{solved}\:{by} \\ $$$${cortano}\:{sir}.\:{why}\:{you}\:{ask}\:{again}? \\ $$
Commented by abdullah_ff last updated on 23/Nov/21
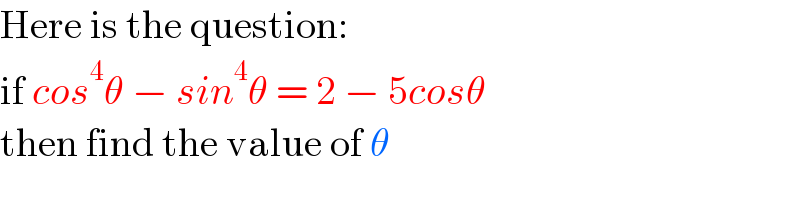
Here is the question: if cos^4 θ − sin^4 θ = 2 − 5cosθ then find the value of θ
$$\mathrm{Here}\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}: \\ $$$$\mathrm{if}\:{cos}^{\mathrm{4}} \theta\:−\:{sin}^{\mathrm{4}} \theta\:=\:\mathrm{2}\:−\:\mathrm{5}{cos}\theta \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\theta \\ $$
Commented by Rasheed.Sindhi last updated on 23/Nov/21
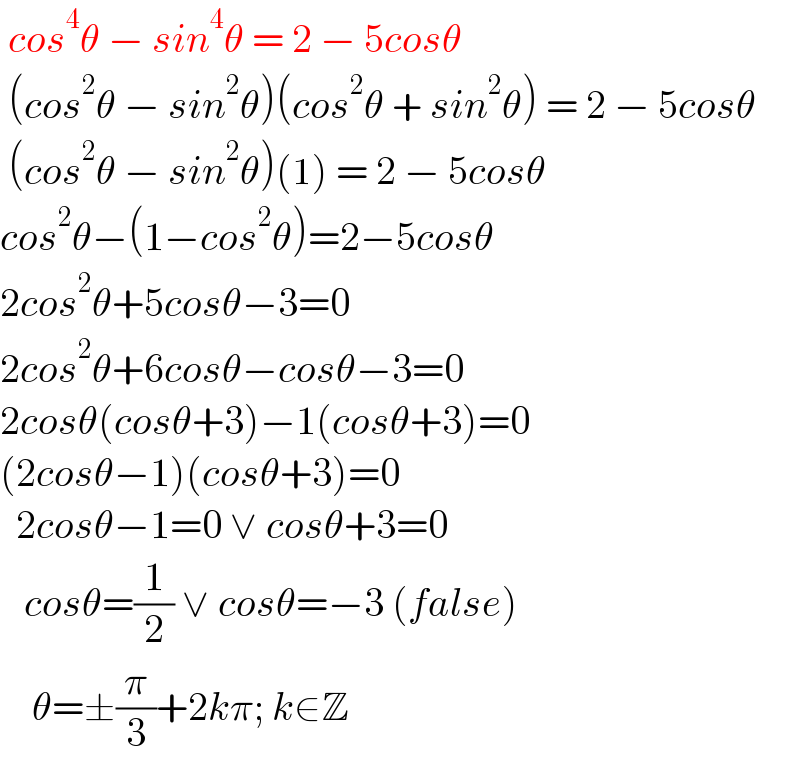
cos^4 θ − sin^4 θ = 2 − 5cosθ (cos^2 θ − sin^2 θ)(cos^2 θ + sin^2 θ) = 2 − 5cosθ (cos^2 θ − sin^2 θ)(1) = 2 − 5cosθ cos^2 θ−(1−cos^2 θ)=2−5cosθ 2cos^2 θ+5cosθ−3=0 2cos^2 θ+6cosθ−cosθ−3=0 2cosθ(cosθ+3)−1(cosθ+3)=0 (2cosθ−1)(cosθ+3)=0 2cosθ−1=0 ∨ cosθ+3=0 cosθ=(1/2) ∨ cosθ=−3 (false) θ=±(π/3)+2kπ; k∈Z
$$\:{cos}^{\mathrm{4}} \theta\:−\:{sin}^{\mathrm{4}} \theta\:=\:\mathrm{2}\:−\:\mathrm{5}{cos}\theta \\ $$$$\:\left({cos}^{\mathrm{2}} \theta\:−\:{sin}^{\mathrm{2}} \theta\right)\left({cos}^{\mathrm{2}} \theta\:+\:{sin}^{\mathrm{2}} \theta\right)\:=\:\mathrm{2}\:−\:\mathrm{5}{cos}\theta \\ $$$$\:\left({cos}^{\mathrm{2}} \theta\:−\:{sin}^{\mathrm{2}} \theta\right)\left(\mathrm{1}\right)\:=\:\mathrm{2}\:−\:\mathrm{5}{cos}\theta \\ $$$${cos}^{\mathrm{2}} \theta−\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)=\mathrm{2}−\mathrm{5}{cos}\theta \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{5}{cos}\theta−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{6}{cos}\theta−{cos}\theta−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{cos}\theta\left({cos}\theta+\mathrm{3}\right)−\mathrm{1}\left({cos}\theta+\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{cos}\theta−\mathrm{1}\right)\left({cos}\theta+\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\:\mathrm{2}{cos}\theta−\mathrm{1}=\mathrm{0}\:\vee\:{cos}\theta+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:{cos}\theta=\frac{\mathrm{1}}{\mathrm{2}}\:\vee\:{cos}\theta=−\mathrm{3}\:\left({false}\right) \\ $$$$\:\:\:\:\theta=\pm\frac{\pi}{\mathrm{3}}+\mathrm{2}{k}\pi;\:{k}\in\mathbb{Z} \\ $$
Commented by abdullah_ff last updated on 23/Nov/21
thanX SiR
$${than}\mathcal{X}\:\:\mathbb{S}{i}\mathbb{R} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Nov/21
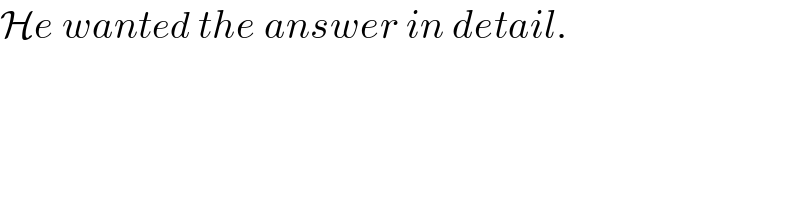
He wanted the answer in detail.
$$\mathcal{H}{e}\:{wanted}\:{the}\:{answer}\:{in}\:{detail}. \\ $$
Commented by abdullah_ff last updated on 23/Nov/21
Dear tounghoungko sir, as Rasheed.Sindhi sir said, I wanted to know the solve of the question in detail. So, I asked to resolve it. But also thanks to cortano sir for his effort and to helping me.
$$\mathrm{Dear}\:\mathrm{tounghoungko}\:\mathrm{sir}, \\ $$$$\mathrm{as}\:\mathrm{Rasheed}.\mathrm{Sindhi}\:\mathrm{sir}\:\mathrm{said},\:{I}\:{wanted} \\ $$$${to}\:{know}\:{the}\:{solve}\:{of}\:{the}\:{question}\:{in} \\ $$$${detail}.\:\mathrm{So},\:\mathrm{I}\:\mathrm{asked}\:\mathrm{to}\:\mathrm{resolve}\:\mathrm{it}. \\ $$$${But}\:{also}\:{thanks}\:{to}\:\mathrm{cortano}\:{sir}\:{for} \\ $$$${his}\:{effort}\:{and}\:{to}\:{helping}\:{me}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *