Menu Close

Can-we-show-a-b-lt-a-2-ab-b-2-a-b-N-

Tinku Tara 0 Comments
Pin




Question Number 182379 by Rasheed.Sindhi last updated on 08/Dec/22
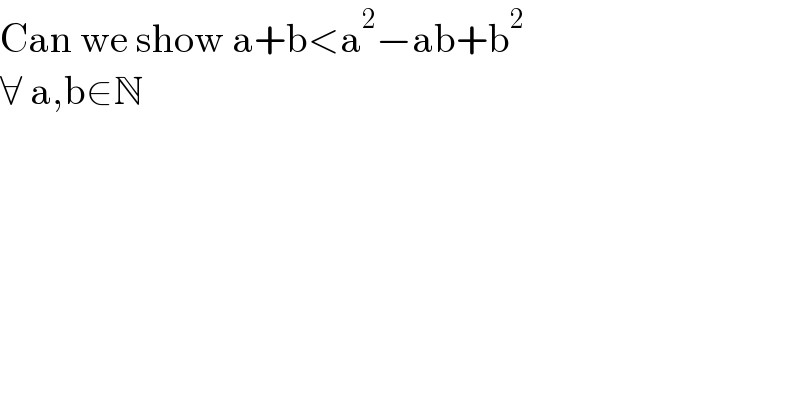
Can we show a+b<a^2 −ab+b^2 ∀ a,b∈N
$$\mathrm{Can}\:\mathrm{we}\:\mathrm{show}\:\mathrm{a}+\mathrm{b}<\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \\ $$$$\forall\:\mathrm{a},\mathrm{b}\in\mathbb{N} \\ $$
Commented by Frix last updated on 08/Dec/22
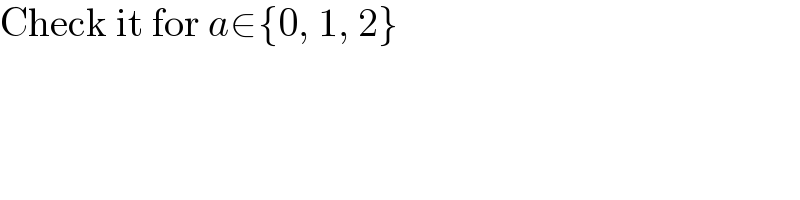
Check it for a∈{0, 1, 2}
$$\mathrm{Check}\:\mathrm{it}\:\mathrm{for}\:{a}\in\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2}\right\} \\ $$
Answered by mr W last updated on 08/Dec/22
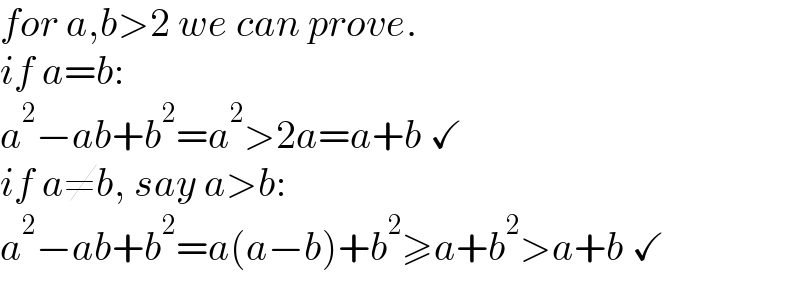
for a,b>2 we can prove. if a=b: a^2 −ab+b^2 =a^2 >2a=a+b ✓ if a≠b, say a>b: a^2 −ab+b^2 =a(a−b)+b^2 ≥a+b^2 >a+b ✓
$${for}\:{a},{b}>\mathrm{2}\:{we}\:{can}\:{prove}. \\ $$$${if}\:{a}={b}: \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} ={a}^{\mathrm{2}} >\mathrm{2}{a}={a}+{b}\:\checkmark \\ $$$${if}\:{a}\neq{b},\:{say}\:{a}>{b}: \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} ={a}\left({a}−{b}\right)+{b}^{\mathrm{2}} \geqslant{a}+{b}^{\mathrm{2}} >{a}+{b}\:\checkmark \\ $$
Commented by Rasheed.Sindhi last updated on 09/Dec/22
ThanX Sir!
$$\boldsymbol{\mathcal{T}{han}\mathcal{X}}\:\boldsymbol{\mathcal{S}{ir}}! \\ $$
Answered by manxsol last updated on 09/Dec/22
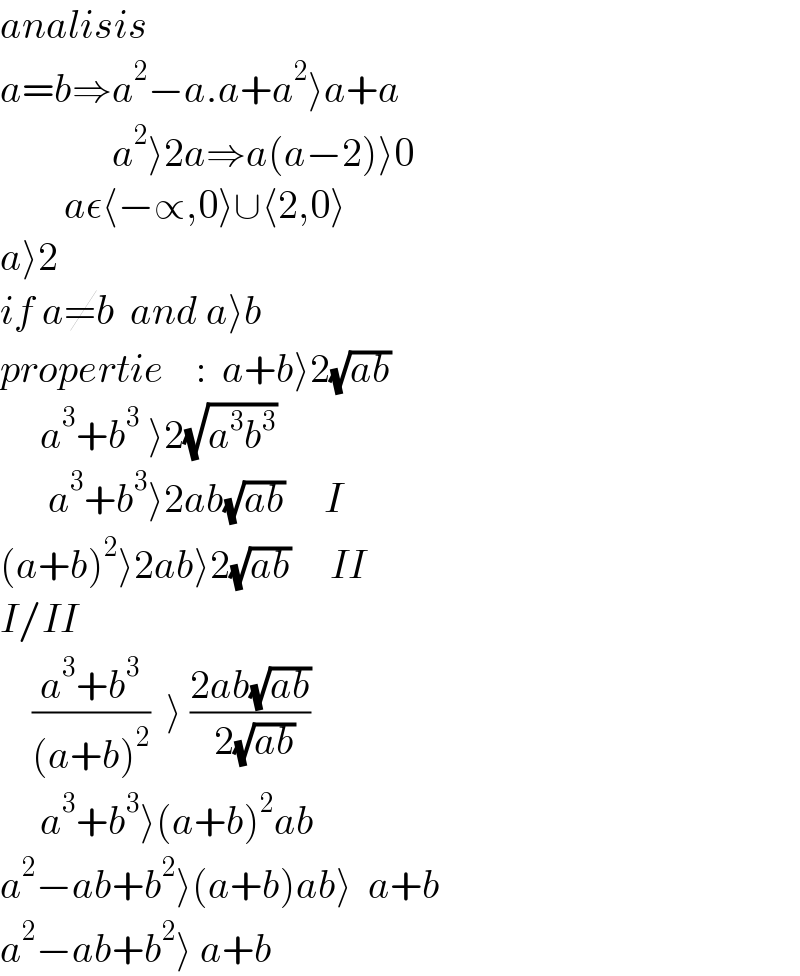
analisis a=b⇒a^2 −a.a+a^2 ⟩a+a a^2 ⟩2a⇒a(a−2)⟩0 aε⟨−∝,0⟩∪⟨2,0⟩ a⟩2 if a≠b and a⟩b propertie : a+b⟩2(√(ab)) a^3 +b^3 ⟩2(√(a^3 b^3 )) a^3 +b^3 ⟩2ab(√(ab)) I (a+b)^2 ⟩2ab⟩2(√(ab)) II I/II ((a^3 +b^3 )/((a+b)^2 )) ⟩ ((2ab(√(ab)))/( 2(√(ab)))) a^3 +b^3 ⟩(a+b)^2 ab a^2 −ab+b^2 ⟩(a+b)ab⟩ a+b a^2 −ab+b^2 ⟩ a+b
$${analisis} \\ $$$${a}={b}\Rightarrow{a}^{\mathrm{2}} −{a}.{a}+{a}^{\mathrm{2}} \rangle{a}+{a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \rangle\mathrm{2}{a}\Rightarrow{a}\left({a}−\mathrm{2}\right)\rangle\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{a}\epsilon\langle−\propto,\mathrm{0}\rangle\cup\langle\mathrm{2},\mathrm{0}\rangle \\ $$$${a}\rangle\mathrm{2} \\ $$$${if}\:{a}\neq{b}\:\:{and}\:{a}\rangle{b} \\ $$$${propertie}\:\:\:\::\:\:{a}+{b}\rangle\mathrm{2}\sqrt{{ab}}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:\rangle\mathrm{2}\sqrt{{a}^{\mathrm{3}} {b}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \rangle\mathrm{2}{ab}\sqrt{{ab}}\:\:\:\:\:{I} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} \rangle\mathrm{2}{ab}\rangle\mathrm{2}\sqrt{{ab}}\:\:\:\:\:{II} \\ $$$${I}/{II} \\ $$$$\:\:\:\:\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{\left({a}+{b}\right)^{\mathrm{2}} }\:\:\rangle\:\frac{\mathrm{2}{ab}\sqrt{{ab}}}{\:\mathrm{2}\sqrt{{ab}}} \\ $$$$\:\:\:\:\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} \rangle\left({a}+{b}\right)^{\mathrm{2}} {ab} \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \rangle\left({a}+{b}\right){ab}\rangle\:\:{a}+{b} \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \rangle\:{a}+{b} \\ $$
Commented by manxsol last updated on 09/Dec/22
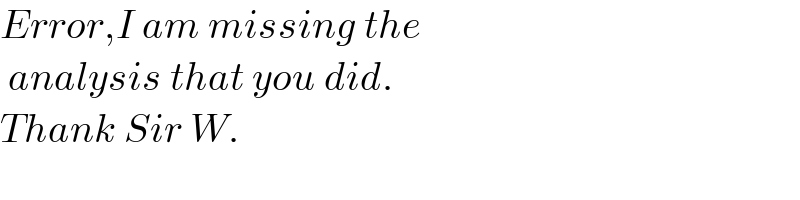
Error,I am missing the analysis that you did. Thank Sir W.
$${Error},{I}\:{am}\:{missing}\:{the} \\ $$$$\:{analysis}\:{that}\:{you}\:{did}. \\ $$$${Thank}\:{Sir}\:{W}. \\ $$
Commented by Rasheed.Sindhi last updated on 09/Dec/22
ThanX Sir!
$$\boldsymbol{\mathcal{T}{han}\mathcal{X}}\:\boldsymbol{\mathcal{S}{ir}}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *