Question Number 171216 by Bagus1003 last updated on 10/Jun/22

$${Can}\:{you}\:{factor}\:: \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$
Commented by MJS_new last updated on 10/Jun/22
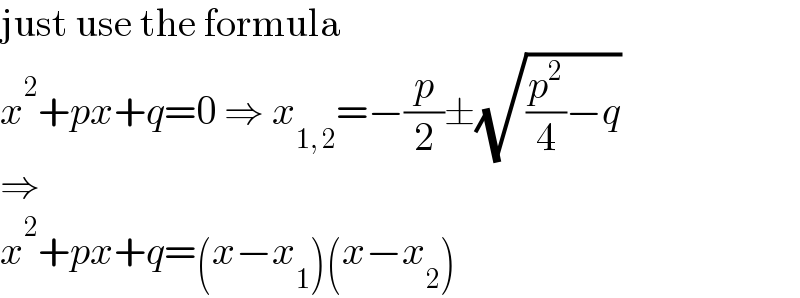
$$\mathrm{just}\:\mathrm{use}\:\mathrm{the}\:\mathrm{formula} \\ $$$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\Rightarrow\:{x}_{\mathrm{1},\:\mathrm{2}} =−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} +{px}+{q}=\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right) \\ $$
Answered by aleks041103 last updated on 10/Jun/22
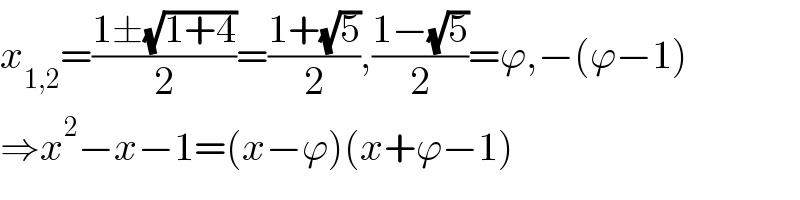
$${x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}=\varphi,−\left(\varphi−\mathrm{1}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{1}=\left({x}−\varphi\right)\left({x}+\varphi−\mathrm{1}\right) \\ $$
