can-you-find-f-x-f-x-f-1-x-x-

Question Number 176083 by Linton last updated on 11/Sep/22

c a n y o u f i n d f (x) ?

f (x) - f (1 - x) = x

Answered by Rasheed.Sindhi last updated on 11/Sep/22

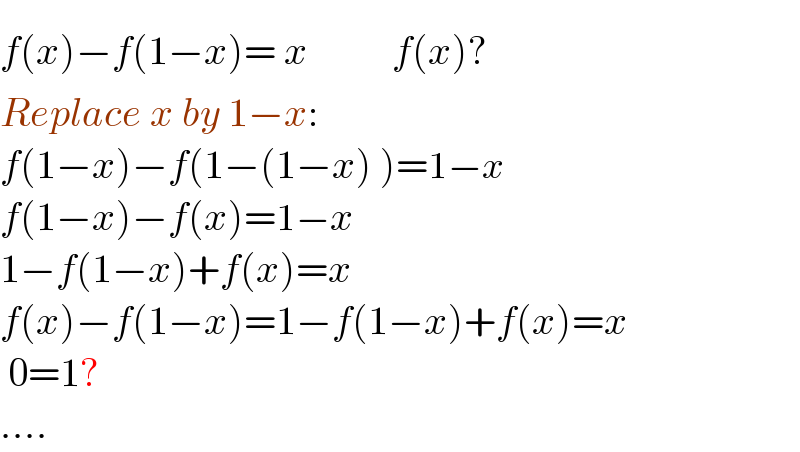
f (x) - f (1 - x) = x f (x) ?

R e p l a c e x b y 1 - x :

f (1 - x) - f (1 - (1 - x)) = 1 - x

f (1 - x) - f (x) = 1 - x

1 - f (1 - x) + f (x) = x

f (x) - f (1 - x) = 1 - f (1 - x) + f (x) = x

0 = 1 ?

\dots .

Answered by Rasheed.Sindhi last updated on 12/Sep/22

f (x) - f (1 - x) = x; f (x) = ?

f (1) - f (0) = 1

f (2) - f (1) = 2

f (3) - f (2) = 3

f (4) - f (3) = 4

\dots .

f (n - 1) - f (n - 2) = n - 1

f (n) - f (n - 1) = n

f (n) - f (0) = \frac{n (n + 1)}{2}

f (n) = \frac{n (n + 1)}{2} + f (0)

A s s u m i n g f (0) = k

f (x) = \frac{x (x + 1)}{2} + k; f (0) = k

Commented by mr W last updated on 12/Sep/22

y o u s o l v e d f (x) - f (x - 1) = x . b u t t h e

q u e s t i o n i s f (x) - f (1 - x) = x .

f (1) - f (0) = 1

f (2) - f (- 1) = 2

f (3) - f (- 2) = 3

\dots

f (x) = \frac{x (x + 1)}{2} + k {d o e s n}^{'} t f u l f i l l t h e

o r i g i n a l e q u a t i o n f (x) - f (1 - x) = x .

a s y o u s h o w e d a b o v e, t h e o r i g i n a l

e q u a t i o n h a s n o s o l u t i o n .

Commented by Rasheed.Sindhi last updated on 12/Sep/22

S o r r y s i r, m y m i s t a k e!

T h a n k y o u v e r y m u c h!