Question Number 50016 by gh.b last updated on 13/Dec/18
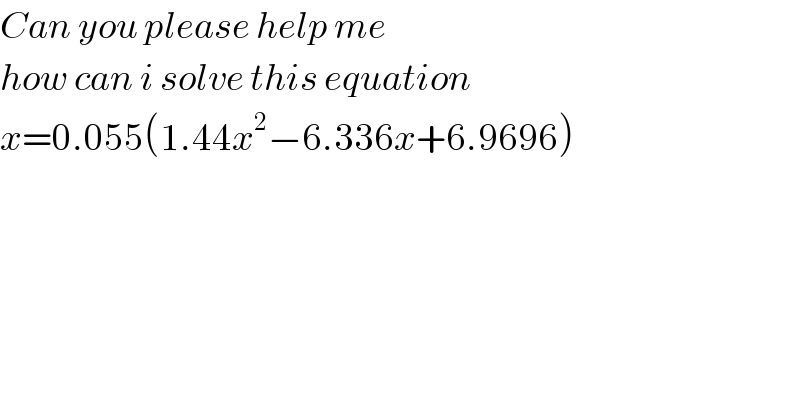
$${Can}\:{you}\:{please}\:{help}\:{me}\: \\ $$$${how}\:{can}\:{i}\:{solve}\:{this}\:{equation}\: \\ $$$${x}=\mathrm{0}.\mathrm{055}\left(\mathrm{1}.\mathrm{44}{x}^{\mathrm{2}} −\mathrm{6}.\mathrm{336}{x}+\mathrm{6}.\mathrm{9696}\right) \\ $$
Answered by MJS last updated on 13/Dec/18

$$\mathrm{its}\:\mathrm{structure}\:\mathrm{is} \\ $$$${x}={a}\left({bx}^{\mathrm{2}} −{cx}+{d}\right) \\ $$$$\mathrm{multiplicate}\:\mathrm{constants} \\ $$$${x}={abx}^{\mathrm{2}} −{acx}+{ad} \\ $$$$\mathrm{bring}\:\mathrm{to}\:\mathrm{one}\:\mathrm{side}\:\mathrm{and}\:\mathrm{transform} \\ $$$${abx}^{\mathrm{2}} −{acx}−{x}+{ad}=\mathrm{0} \\ $$$${abx}^{\mathrm{2}} −\left({ac}+\mathrm{1}\right){x}+{ad}=\mathrm{0} \\ $$$$\mathrm{use}\:\mathrm{formula} \\ $$$${Ax}^{\mathrm{2}} +{Bx}+{C}=\mathrm{0}\:\Leftrightarrow\:{x}=\frac{−{B}\pm\sqrt{{B}^{\mathrm{2}} −\mathrm{4}{AC}}}{\mathrm{2}{A}} \\ $$$$\mathrm{with}\:{A}={ab},\:{B}=−\left({ac}+\mathrm{1}\right),\:{C}={ad} \\ $$
Answered by peter frank last updated on 13/Dec/18
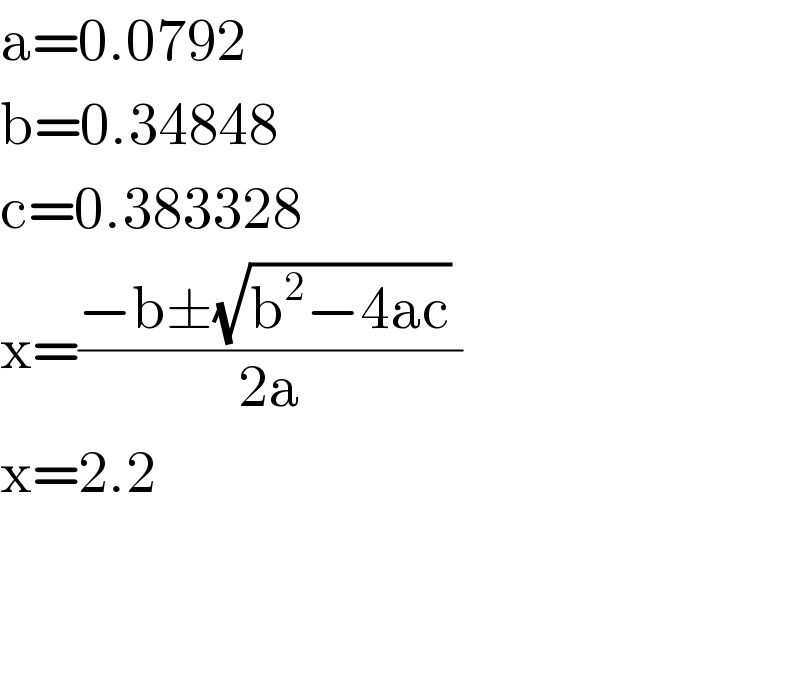
$$\mathrm{a}=\mathrm{0}.\mathrm{0792} \\ $$$$\mathrm{b}=\mathrm{0}.\mathrm{34848} \\ $$$$\mathrm{c}=\mathrm{0}.\mathrm{383328} \\ $$$$\mathrm{x}=\frac{−\mathrm{b}\pm\sqrt{\mathrm{b}^{\mathrm{2}} −\mathrm{4ac}}\:}{\mathrm{2a}} \\ $$$$\mathrm{x}=\mathrm{2}.\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
