Question Number 55174 by gunawan last updated on 18/Feb/19

$$\mathrm{center}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{convergence} \\ $$$$\:\mathrm{of}\:\mathrm{series}\:\underset{{n}=\mathrm{0}} {\overset{\propto} {\Sigma}}\:\left(\frac{\mathrm{4}−\mathrm{2}{i}}{\mathrm{1}+\mathrm{5}{i}}\right)^{{n}} {z}^{{n}} \:\mathrm{is}… \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 19/Feb/19
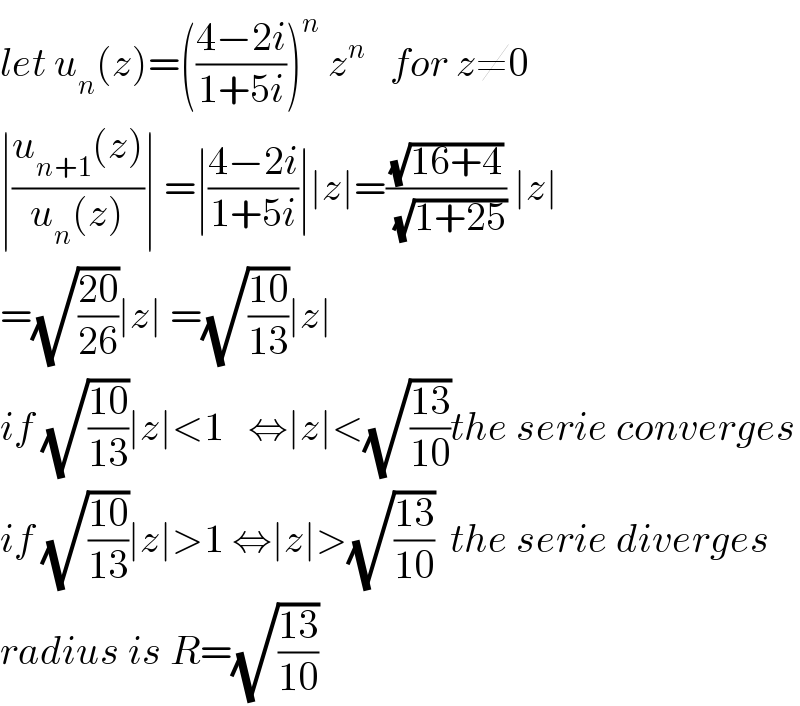
$${let}\:{u}_{{n}} \left({z}\right)=\left(\frac{\mathrm{4}−\mathrm{2}{i}}{\mathrm{1}+\mathrm{5}{i}}\right)^{{n}} \:{z}^{{n}} \:\:\:{for}\:{z}\neq\mathrm{0} \\ $$$$\mid\frac{{u}_{{n}+\mathrm{1}} \left({z}\right)}{{u}_{{n}} \left({z}\right)}\mid\:=\mid\frac{\mathrm{4}−\mathrm{2}{i}}{\mathrm{1}+\mathrm{5}{i}}\mid\mid{z}\mid=\frac{\sqrt{\mathrm{16}+\mathrm{4}}}{\:\sqrt{\mathrm{1}+\mathrm{25}}}\:\mid{z}\mid \\ $$$$=\sqrt{\frac{\mathrm{20}}{\mathrm{26}}}\mid{z}\mid\:=\sqrt{\frac{\mathrm{10}}{\mathrm{13}}}\mid{z}\mid \\ $$$${if}\:\sqrt{\frac{\mathrm{10}}{\mathrm{13}}}\mid{z}\mid<\mathrm{1}\:\:\:\Leftrightarrow\mid{z}\mid<\sqrt{\frac{\mathrm{13}}{\mathrm{10}}}{the}\:{serie}\:{converges} \\ $$$${if}\:\sqrt{\frac{\mathrm{10}}{\mathrm{13}}}\mid{z}\mid>\mathrm{1}\:\Leftrightarrow\mid{z}\mid>\sqrt{\frac{\mathrm{13}}{\mathrm{10}}}\:\:{the}\:{serie}\:{diverges} \\ $$$${radius}\:{is}\:{R}=\sqrt{\frac{\mathrm{13}}{\mathrm{10}}} \\ $$
Commented by gunawan last updated on 19/Feb/19

$$\mathrm{wow} \\ $$$$\mathrm{thanks}\:\mathrm{Sir} \\ $$
Commented by maxmathsup by imad last updated on 19/Feb/19
$${you}\:{are}\:{welcome}. \\ $$
