Question Number 126139 by mnjuly1970 last updated on 17/Dec/20
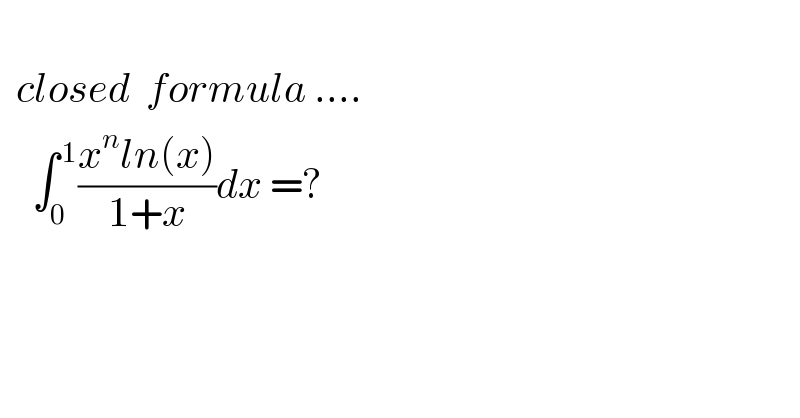
$$\:\:\:\:\:\:\: \\ $$$$\:\:{closed}\:\:{formula}\:…. \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}} {ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}\:=? \\ $$$$\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 17/Dec/20
![Σ_(k=0) ^∞ (−1)^n ∫_0 ^1 x^n x^k log(x)dx =Σ_(k=0) ^∞ (−1)^k [log(x)(x^(n+k+1) /(n+k+1))]_0 ^1 −∫_0 ^1 (x^(n+k) /((n+k+1)))dx =Σ_(k=0) ^∞ (−1)^(k+1) (1/((n+k+1)^2 ))=−(1/((n+1+0)^2 ))+(1/((n+1+1)^2 ))−(1/((n+3)^2 ))+..=S (1/((n+1)^2 ))+(1/((n+2)^2 ))+(1/((n+3)^2 ))+..=ζ(2,n+1) S+ζ(2,n+1)=2((1/((n+2)^2 ))+(1/((n+4)^2 ))+....) S+ζ(2,n)=(1/2)Σ_(k=1) ^∞ (1/(((n/2)+k)^2 ))=(1/2)ζ(2,(n/2))−(2/n^2 ) S=(1/2)ζ(2,(n/2))−ζ(2,n+1)−(2/n^2 ) Note:Σ_(n=0) ^∞ (1/((n+k)^s ))=ζ(s,k) (Hurwitz zeta)](https://www.tinkutara.com/question/Q126142.png)
$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {x}^{{k}} {log}\left({x}\right){dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \left[{log}\left({x}\right)\frac{{x}^{{n}+{k}+\mathrm{1}} }{{n}+{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+{k}} }{\left({n}+{k}+\mathrm{1}\right)}{dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \frac{\mathrm{1}}{\left({n}+{k}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\mathrm{0}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }+..={S} \\ $$$$\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{3}\right)^{\mathrm{2}} }+..=\zeta\left(\mathrm{2},{n}+\mathrm{1}\right) \\ $$$${S}+\zeta\left(\mathrm{2},{n}+\mathrm{1}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{4}\right)^{\mathrm{2}} }+….\right) \\ $$$${S}+\zeta\left(\mathrm{2},{n}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\frac{{n}}{\mathrm{2}}+{k}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2},\frac{{n}}{\mathrm{2}}\right)−\frac{\mathrm{2}}{{n}^{\mathrm{2}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2},\frac{{n}}{\mathrm{2}}\right)−\zeta\left(\mathrm{2},{n}+\mathrm{1}\right)−\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\:\boldsymbol{{Note}}:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{k}\right)^{{s}} }=\zeta\left({s},{k}\right)\:\left({Hurwitz}\:{zeta}\right) \\ $$
Commented by mnjuly1970 last updated on 17/Dec/20
$${thank}\:\:{you}\:{so}\:{much}.. \\ $$
Commented by Dwaipayan Shikari last updated on 17/Dec/20
$${But}\:{the}\:{question}\:{seems}\:{to}\:{be}\:{deleted} \\ $$
Commented by mnjuly1970 last updated on 17/Dec/20
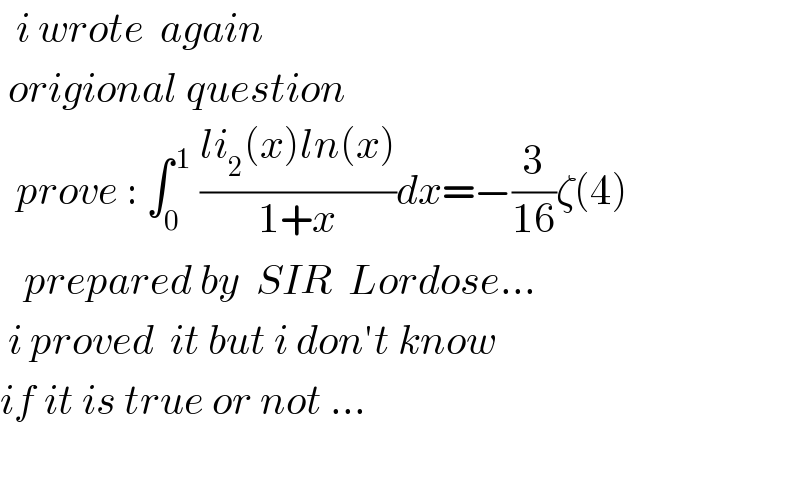
$$\:\:{i}\:{wrote}\:\:{again} \\ $$$$\:{origional}\:{question}\: \\ $$$$\:\:{prove}\::\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{li}_{\mathrm{2}} \left({x}\right){ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}=−\frac{\mathrm{3}}{\mathrm{16}}\zeta\left(\mathrm{4}\right) \\ $$$$\:\:\:{prepared}\:{by}\:\:{SIR}\:\:{Lordose}… \\ $$$$\:{i}\:{proved}\:\:{it}\:{but}\:{i}\:{don}'{t}\:{know} \\ $$$${if}\:{it}\:{is}\:{true}\:{or}\:{not}\:… \\ $$$$\: \\ $$
Answered by mathmax by abdo last updated on 17/Dec/20
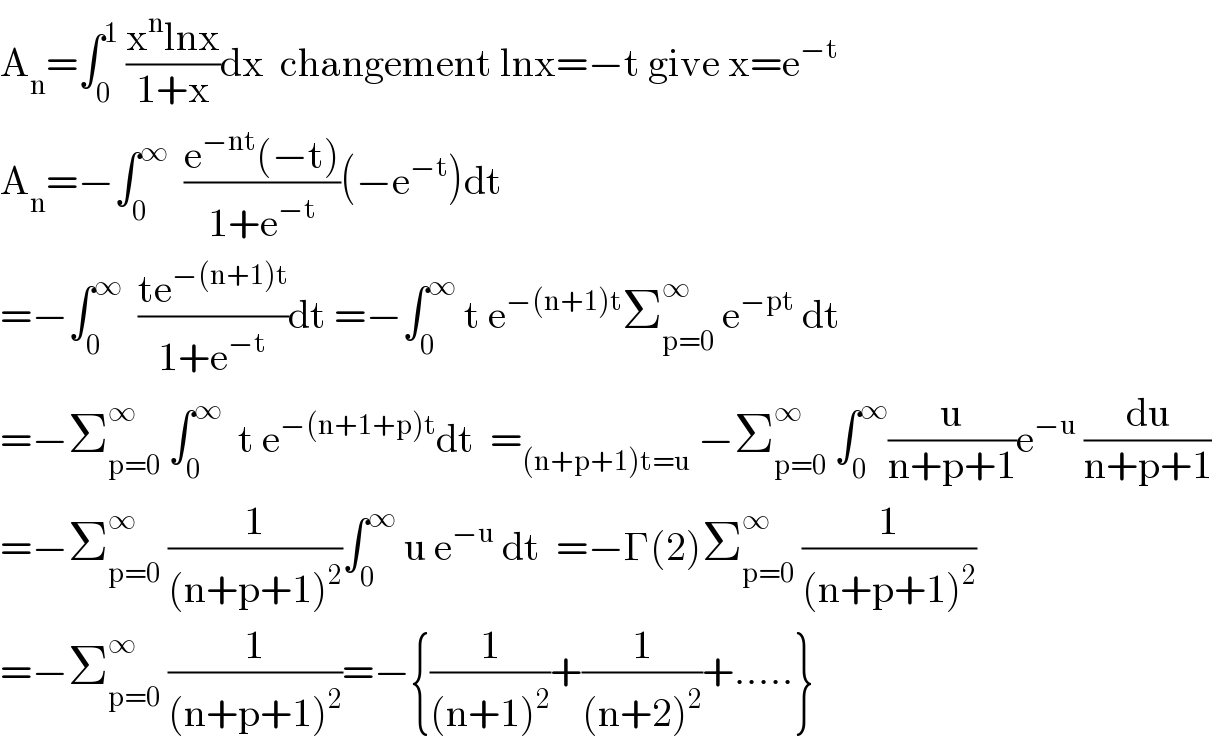
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} \mathrm{lnx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}=−\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{e}^{−\mathrm{t}} \\ $$$$\mathrm{A}_{\mathrm{n}} =−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{nt}} \left(−\mathrm{t}\right)}{\mathrm{1}+\mathrm{e}^{−\mathrm{t}} }\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{te}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{t}} }\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{pt}} \:\mathrm{dt} \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}\:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}+\mathrm{p}\right)\mathrm{t}} \mathrm{dt}\:\:=_{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)\mathrm{t}=\mathrm{u}} \:−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}}{\mathrm{n}+\mathrm{p}+\mathrm{1}}\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\mathrm{n}+\mathrm{p}+\mathrm{1}} \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}\:\mathrm{e}^{−\mathrm{u}} \:\mathrm{dt}\:\:=−\Gamma\left(\mathrm{2}\right)\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} }=−\left\{\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} }+…..\right\} \\ $$
