Menu Close

closest-distance-point-6-9-to-curve-y-x-2-12x-32-mister-w-your-method-can-be-applied-to-this-problem-

Tinku Tara 0 Comments
Pin




Question Number 83520 by john santu last updated on 03/Mar/20
closest distance point (6,9) to curve y = x^2 −12x+32 . mister w your method can be applied to this problem?
$$\mathrm{closest}\:\mathrm{distance}\:\mathrm{point}\:\left(\mathrm{6},\mathrm{9}\right)\: \\ $$$$\mathrm{to}\:\mathrm{curve}\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{12x}+\mathrm{32}\:. \\ $$$$\mathrm{mister}\:\mathrm{w}\:\mathrm{your}\:\mathrm{method}\:\mathrm{can}\:\mathrm{be}\: \\ $$$$\mathrm{applied}\:\mathrm{to}\:\mathrm{this}\:\mathrm{problem}? \\ $$
Answered by john santu last updated on 03/Mar/20
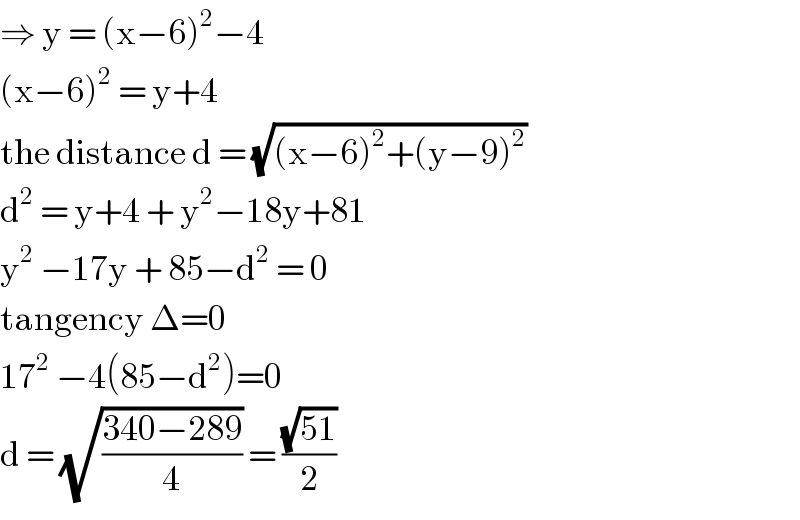
⇒ y = (x−6)^2 −4 (x−6)^2 = y+4 the distance d = (√((x−6)^2 +(y−9)^2 )) d^2 = y+4 + y^2 −18y+81 y^2 −17y + 85−d^2 = 0 tangency Δ=0 17^2 −4(85−d^2 )=0 d = (√((340−289)/4)) = ((√(51))/2)
$$\Rightarrow\:\mathrm{y}\:=\:\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{4} \\ $$$$\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} \:=\:\mathrm{y}+\mathrm{4} \\ $$$$\mathrm{the}\:\mathrm{distance}\:\mathrm{d}\:=\:\sqrt{\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{d}^{\mathrm{2}} \:=\:\mathrm{y}+\mathrm{4}\:+\:\mathrm{y}^{\mathrm{2}} −\mathrm{18y}+\mathrm{81} \\ $$$$\mathrm{y}^{\mathrm{2}} \:−\mathrm{17y}\:+\:\mathrm{85}−\mathrm{d}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{tangency}\:\Delta=\mathrm{0} \\ $$$$\mathrm{17}^{\mathrm{2}} \:−\mathrm{4}\left(\mathrm{85}−\mathrm{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{d}\:=\:\sqrt{\frac{\mathrm{340}−\mathrm{289}}{\mathrm{4}}}\:=\:\frac{\sqrt{\mathrm{51}}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 03/Mar/20
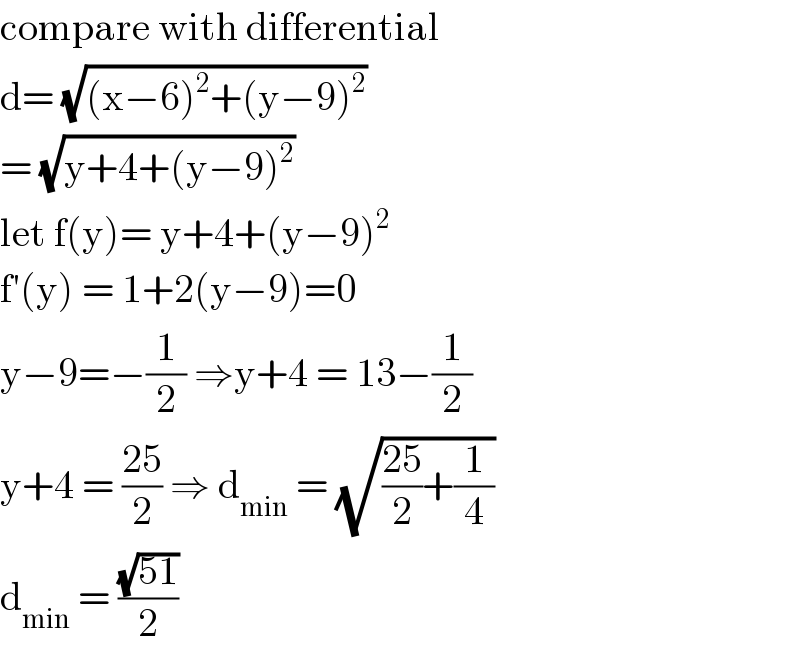
compare with differential d= (√((x−6)^2 +(y−9)^2 )) = (√(y+4+(y−9)^2 )) let f(y)= y+4+(y−9)^2 f′(y) = 1+2(y−9)=0 y−9=−(1/2) ⇒y+4 = 13−(1/2) y+4 = ((25)/2) ⇒ d_(min) = (√(((25)/2)+(1/4))) d_(min) = ((√(51))/2)
$$\mathrm{compare}\:\mathrm{with}\:\mathrm{differential} \\ $$$$\mathrm{d}=\:\sqrt{\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{9}\right)^{\mathrm{2}} }\: \\ $$$$=\:\sqrt{\mathrm{y}+\mathrm{4}+\left(\mathrm{y}−\mathrm{9}\right)^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{y}\right)=\:\mathrm{y}+\mathrm{4}+\left(\mathrm{y}−\mathrm{9}\right)^{\mathrm{2}} \\ $$$$\mathrm{f}'\left(\mathrm{y}\right)\:=\:\mathrm{1}+\mathrm{2}\left(\mathrm{y}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{y}−\mathrm{9}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{y}+\mathrm{4}\:=\:\mathrm{13}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{y}+\mathrm{4}\:=\:\frac{\mathrm{25}}{\mathrm{2}}\:\Rightarrow\:\mathrm{d}_{\mathrm{min}} \:=\:\sqrt{\frac{\mathrm{25}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{d}_{\mathrm{min}} \:=\:\frac{\sqrt{\mathrm{51}}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 03/Mar/20
good!
$${good}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *