Menu Close

coeff-of-x-2-from-6-8x-3-2-x-2-5-

Tinku Tara 0 Comments
Pin




Question Number 176276 by cortano1 last updated on 15/Sep/22
coeff of x^2 from [6+8x−(3/2)x^2 ]^5
$$\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{from}\: \\ $$$$\:\:\left[\mathrm{6}+\mathrm{8x}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:\right]^{\mathrm{5}} \: \\ $$
Answered by mr W last updated on 15/Sep/22
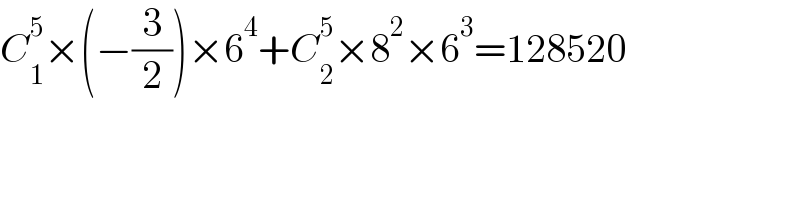
C_1 ^5 ×(−(3/2))×6^4 +C_2 ^5 ×8^2 ×6^3 =128520
$${C}_{\mathrm{1}} ^{\mathrm{5}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)×\mathrm{6}^{\mathrm{4}} +{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{8}^{\mathrm{2}} ×\mathrm{6}^{\mathrm{3}} =\mathrm{128520} \\ $$
Commented by cortano1 last updated on 16/Sep/22
nice .
$$\mathrm{nice}\:.\: \\ $$
Commented by cortano1 last updated on 16/Sep/22
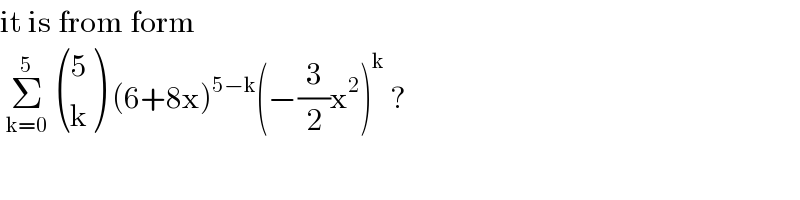
it is from form Σ_(k=0) ^5 ((5),(k) ) (6+8x)^(5−k) (−(3/2)x^2 )^k ?
$$\mathrm{it}\:\mathrm{is}\:\mathrm{from}\:\mathrm{form}\: \\ $$$$\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{k}}\end{pmatrix}\:\left(\mathrm{6}+\mathrm{8x}\right)^{\mathrm{5}−\mathrm{k}} \left(−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{k}} \:? \\ $$
Commented by mr W last updated on 16/Sep/22
no, i applied no formula. to get x^2 we need 1. one term −(3/2)x^2 and 4 terms 6, to select the term −(3/2)x^2 , there are C_1 ^5 ways, therefore we get C_1 ^5 ×(−(3/2))×6^4 . 2. two terms 8x and 3 terms 6, to select two terms 8x , there are C_2 ^5 ways, therefore we get C_2 ^5 ×8^2 ×6^3 . totally we get C_1 ^5 ×(−(3/2))×6^4 +C_2 ^5 ×8^2 ×6^3
$${no},\:{i}\:{applied}\:{no}\:{formula}. \\ $$$${to}\:{get}\:{x}^{\mathrm{2}} \:{we}\:{need} \\ $$$$\mathrm{1}.\:{one}\:{term}\:−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \:{and}\:\mathrm{4}\:{terms}\:\mathrm{6}, \\ $$$$\:\:\:\:\:{to}\:{select}\:{the}\:{term}\:−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} ,\:{there}\:{are} \\ $$$$\:\:\:\:\:{C}_{\mathrm{1}} ^{\mathrm{5}} \:{ways},\:{therefore}\:{we}\:{get} \\ $$$$\:\:\:\:\:{C}_{\mathrm{1}} ^{\mathrm{5}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)×\mathrm{6}^{\mathrm{4}} . \\ $$$$\mathrm{2}.\:\:{two}\:{terms}\:\mathrm{8}{x}\:{and}\:\mathrm{3}\:{terms}\:\mathrm{6}, \\ $$$$\:\:\:\:\:{to}\:{select}\:{two}\:{terms}\:\mathrm{8}{x}\:,\:{there}\:{are} \\ $$$$\:\:\:\:\:{C}_{\mathrm{2}} ^{\mathrm{5}} \:{ways},\:{therefore}\:{we}\:{get} \\ $$$$\:\:\:\:\:{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{8}^{\mathrm{2}} ×\mathrm{6}^{\mathrm{3}} . \\ $$$${totally}\:{we}\:{get} \\ $$$${C}_{\mathrm{1}} ^{\mathrm{5}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)×\mathrm{6}^{\mathrm{4}} +{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{8}^{\mathrm{2}} ×\mathrm{6}^{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 18/Sep/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 16/Sep/22
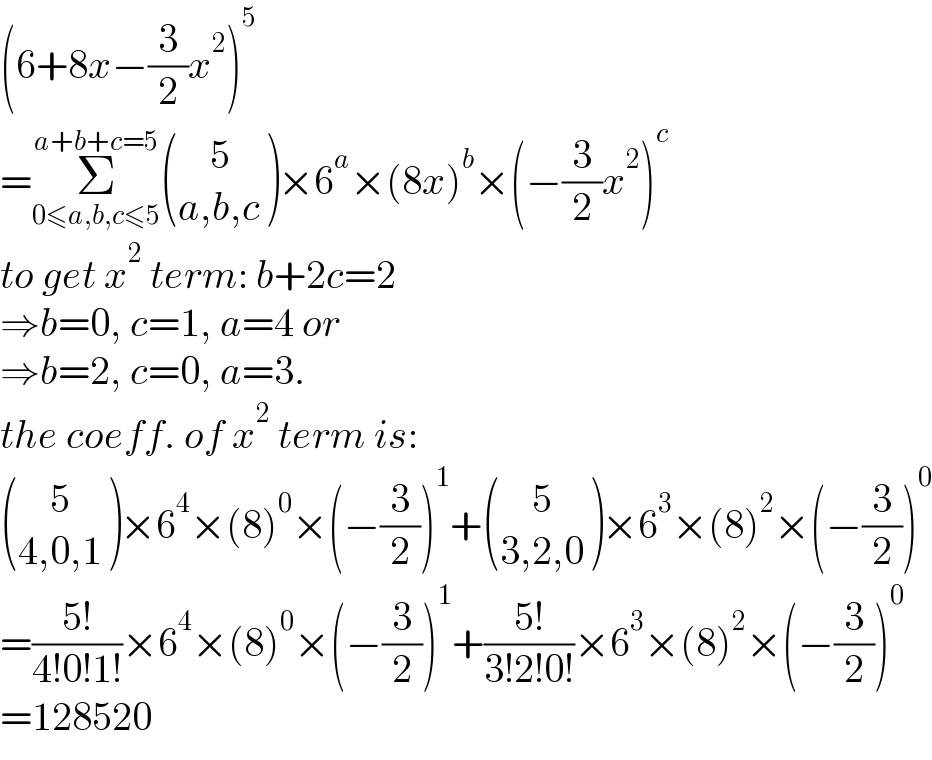
(6+8x−(3/2)x^2 )^5 =Σ_(0≤a,b,c≤5) ^(a+b+c=5) ((( 5)),((a,b,c)) )×6^a ×(8x)^b ×(−(3/2)x^2 )^c to get x^2 term: b+2c=2 ⇒b=0, c=1, a=4 or ⇒b=2, c=0, a=3. the coeff. of x^2 term is: ((( 5)),((4,0,1)) )×6^4 ×(8)^0 ×(−(3/2))^1 + ((( 5)),((3,2,0)) )×6^3 ×(8)^2 ×(−(3/2))^0 =((5!)/(4!0!1!))×6^4 ×(8)^0 ×(−(3/2))^1 +((5!)/(3!2!0!))×6^3 ×(8)^2 ×(−(3/2))^0 =128520
$$\left(\mathrm{6}+\mathrm{8}{x}−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right)^{\mathrm{5}} \\ $$$$=\underset{\mathrm{0}\leqslant{a},{b},{c}\leqslant\mathrm{5}} {\overset{{a}+{b}+{c}=\mathrm{5}} {\sum}}\begin{pmatrix}{\:\:\:\:\mathrm{5}}\\{{a},{b},{c}}\end{pmatrix}×\mathrm{6}^{{a}} ×\left(\mathrm{8}{x}\right)^{{b}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right)^{{c}} \\ $$$${to}\:{get}\:{x}^{\mathrm{2}} \:{term}:\:{b}+\mathrm{2}{c}=\mathrm{2} \\ $$$$\Rightarrow{b}=\mathrm{0},\:{c}=\mathrm{1},\:{a}=\mathrm{4}\:{or} \\ $$$$\Rightarrow{b}=\mathrm{2},\:{c}=\mathrm{0},\:{a}=\mathrm{3}. \\ $$$${the}\:{coeff}.\:{of}\:{x}^{\mathrm{2}} \:{term}\:{is}: \\ $$$$\begin{pmatrix}{\:\:\:\:\mathrm{5}}\\{\mathrm{4},\mathrm{0},\mathrm{1}}\end{pmatrix}×\mathrm{6}^{\mathrm{4}} ×\left(\mathrm{8}\right)^{\mathrm{0}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{1}} +\begin{pmatrix}{\:\:\:\:\mathrm{5}}\\{\mathrm{3},\mathrm{2},\mathrm{0}}\end{pmatrix}×\mathrm{6}^{\mathrm{3}} ×\left(\mathrm{8}\right)^{\mathrm{2}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{0}} \\ $$$$=\frac{\mathrm{5}!}{\mathrm{4}!\mathrm{0}!\mathrm{1}!}×\mathrm{6}^{\mathrm{4}} ×\left(\mathrm{8}\right)^{\mathrm{0}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{1}} +\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!\mathrm{0}!}×\mathrm{6}^{\mathrm{3}} ×\left(\mathrm{8}\right)^{\mathrm{2}} ×\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{0}} \\ $$$$=\mathrm{128520} \\ $$
Commented by Tawa11 last updated on 25/Sep/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *