Question Number 103513 by bemath last updated on 15/Jul/20
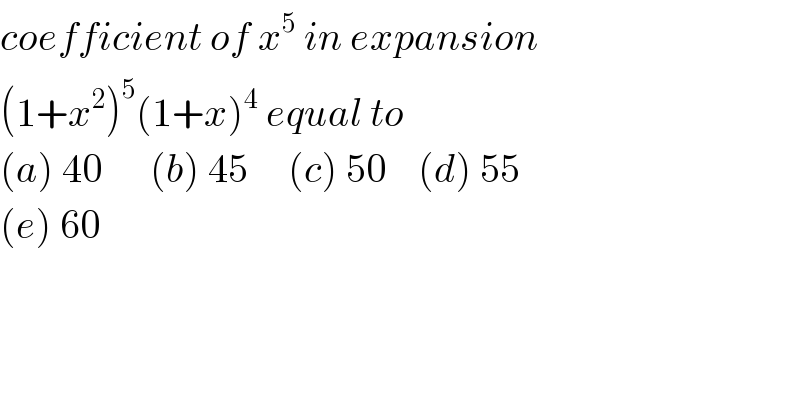
$${coefficient}\:{of}\:{x}^{\mathrm{5}} \:{in}\:{expansion} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{5}} \left(\mathrm{1}+{x}\right)^{\mathrm{4}} \:{equal}\:{to}\: \\ $$$$\left({a}\right)\:\mathrm{40}\:\:\:\:\:\:\left({b}\right)\:\mathrm{45}\:\:\:\:\:\left({c}\right)\:\mathrm{50}\:\:\:\:\left({d}\right)\:\mathrm{55} \\ $$$$\left({e}\right)\:\mathrm{60} \\ $$
Answered by OlafThorendsen last updated on 15/Jul/20
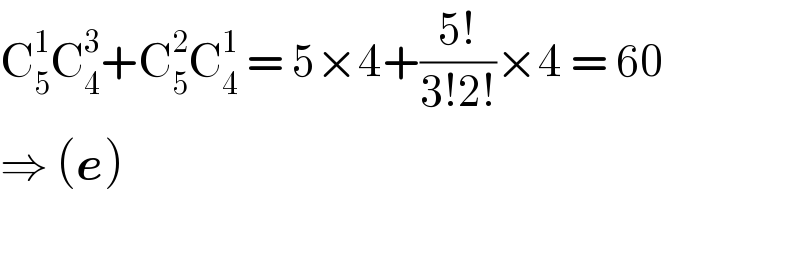
$$\mathrm{C}_{\mathrm{5}} ^{\mathrm{1}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{3}} +\mathrm{C}_{\mathrm{5}} ^{\mathrm{2}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} \:=\:\mathrm{5}×\mathrm{4}+\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}×\mathrm{4}\:=\:\mathrm{60} \\ $$$$\Rightarrow\:\left(\boldsymbol{{e}}\right) \\ $$$$ \\ $$
Commented by bemath last updated on 15/Jul/20

$${how}\:{do}\:{you}\:{got}\:{it}\:? \\ $$
Commented by OlafThorendsen last updated on 15/Jul/20
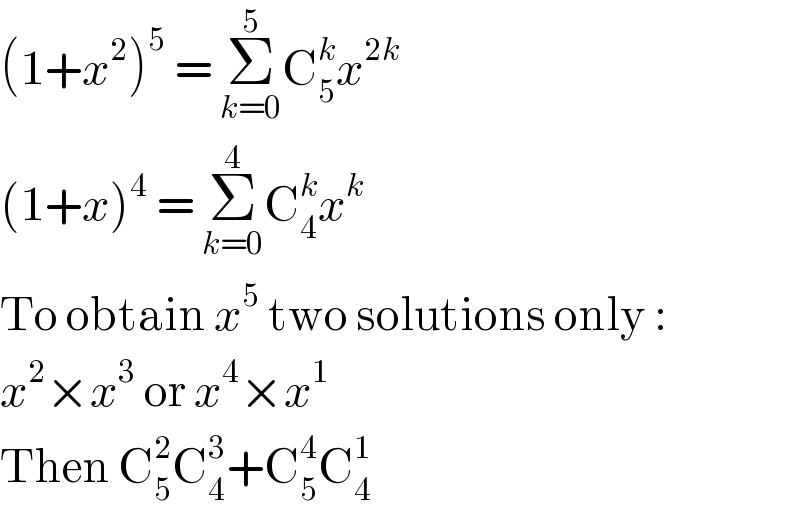
$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{5}} \:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\mathrm{C}_{\mathrm{5}} ^{{k}} {x}^{\mathrm{2}{k}} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{4}} \:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}\mathrm{C}_{\mathrm{4}} ^{{k}} {x}^{{k}} \\ $$$$\mathrm{To}\:\mathrm{obtain}\:{x}^{\mathrm{5}} \:\mathrm{two}\:\mathrm{solutions}\:\mathrm{only}\:: \\ $$$${x}^{\mathrm{2}} ×{x}^{\mathrm{3}} \:\mathrm{or}\:{x}^{\mathrm{4}} ×{x}^{\mathrm{1}} \\ $$$$\mathrm{Then}\:\mathrm{C}_{\mathrm{5}} ^{\mathrm{2}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{3}} +\mathrm{C}_{\mathrm{5}} ^{\mathrm{4}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} \\ $$
Answered by Rio Michael last updated on 15/Jul/20
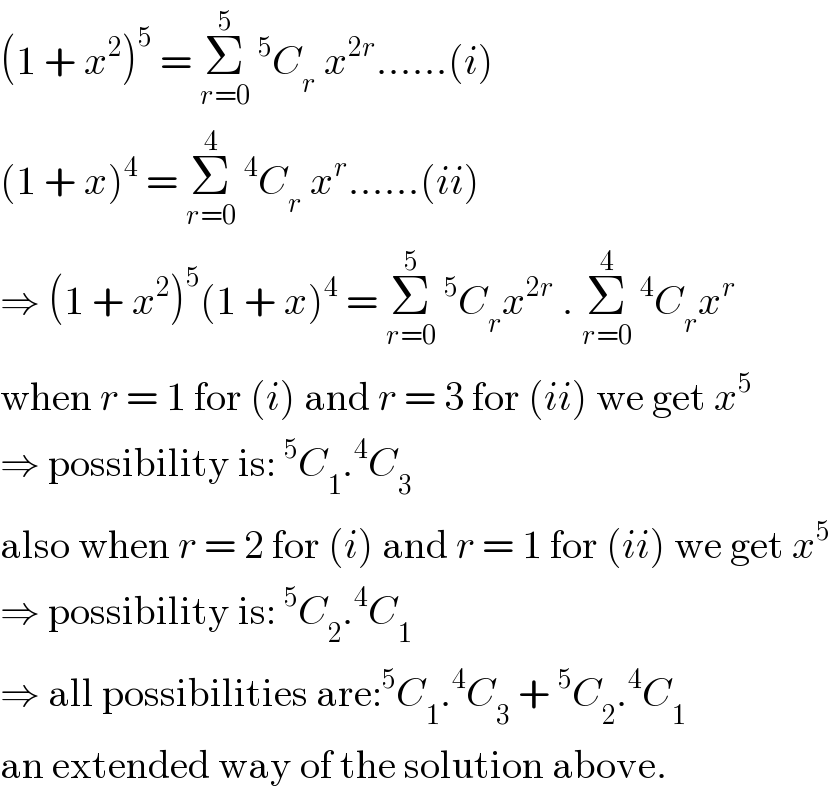
$$\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)^{\mathrm{5}} \:=\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\:^{\mathrm{5}} {C}_{{r}} \:{x}^{\mathrm{2}{r}} ……\left({i}\right) \\ $$$$\left(\mathrm{1}\:+\:{x}\right)^{\mathrm{4}} \:=\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}\:^{\mathrm{4}} {C}_{{r}} \:{x}^{{r}} ……\left({ii}\right) \\ $$$$\Rightarrow\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)^{\mathrm{5}} \left(\mathrm{1}\:+\:{x}\right)^{\mathrm{4}} \:=\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\:^{\mathrm{5}} {C}_{{r}} {x}^{\mathrm{2}{r}} \:.\:\underset{{r}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}\:^{\mathrm{4}} {C}_{{r}} {x}^{{r}} \: \\ $$$$\mathrm{when}\:{r}\:=\:\mathrm{1}\:\mathrm{for}\:\left({i}\right)\:\mathrm{and}\:{r}\:=\:\mathrm{3}\:\mathrm{for}\:\left({ii}\right)\:\mathrm{we}\:\mathrm{get}\:{x}^{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{possibility}\:\mathrm{is}:\:^{\mathrm{5}} {C}_{\mathrm{1}} .^{\mathrm{4}} {C}_{\mathrm{3}} \\ $$$$\mathrm{also}\:\mathrm{when}\:{r}\:=\:\mathrm{2}\:\mathrm{for}\:\left({i}\right)\:\mathrm{and}\:{r}\:=\:\mathrm{1}\:\mathrm{for}\:\left({ii}\right)\:\mathrm{we}\:\mathrm{get}\:{x}^{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{possibility}\:\mathrm{is}:\:^{\mathrm{5}} {C}_{\mathrm{2}} .^{\mathrm{4}} {C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{all}\:\mathrm{possibilities}\:\mathrm{are}:^{\mathrm{5}} {C}_{\mathrm{1}} .^{\mathrm{4}} {C}_{\mathrm{3}} \:+\:^{\mathrm{5}} {C}_{\mathrm{2}} .^{\mathrm{4}} {C}_{\mathrm{1}} \\ $$$$\mathrm{an}\:\mathrm{extended}\:\mathrm{way}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{above}. \\ $$
