Question Number 176300 by cortano1 last updated on 16/Sep/22
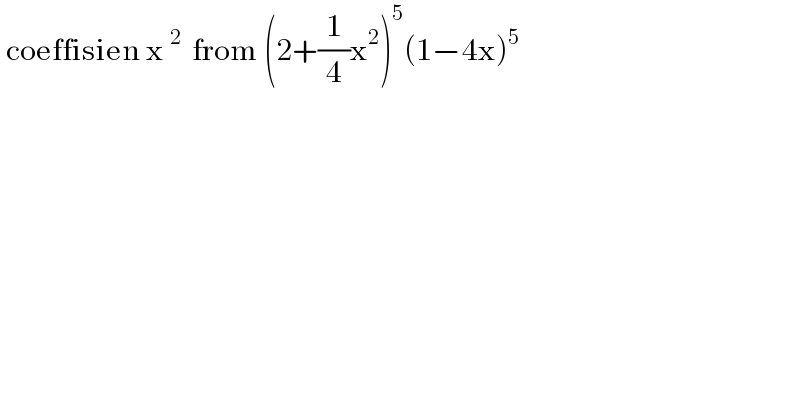
$$\:\mathrm{coeffisien}\:\mathrm{x}\:^{\mathrm{2}\:} \:\mathrm{from}\:\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{5}} \left(\mathrm{1}−\mathrm{4x}\right)^{\mathrm{5}} \\ $$
Commented by mr W last updated on 16/Sep/22
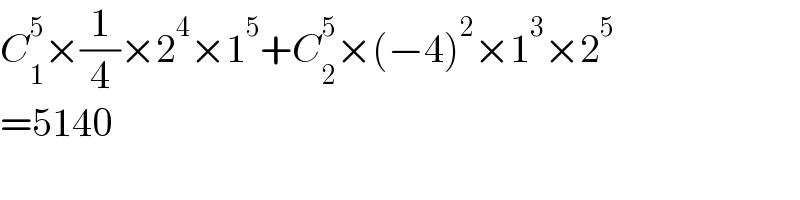
$${C}_{\mathrm{1}} ^{\mathrm{5}} ×\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2}^{\mathrm{4}} ×\mathrm{1}^{\mathrm{5}} +{C}_{\mathrm{2}} ^{\mathrm{5}} ×\left(−\mathrm{4}\right)^{\mathrm{2}} ×\mathrm{1}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{5}} \\ $$$$=\mathrm{5140} \\ $$
Commented by Ari last updated on 16/Sep/22
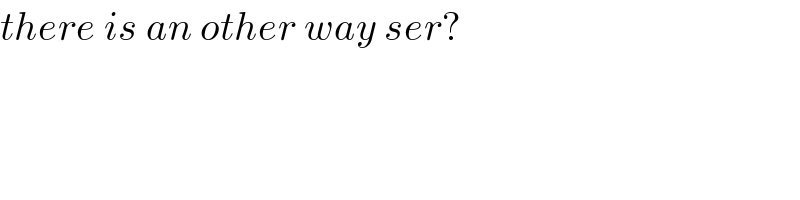
$${there}\:{is}\:{an}\:{other}\:{way}\:{ser}? \\ $$
Commented by mr W last updated on 16/Sep/22
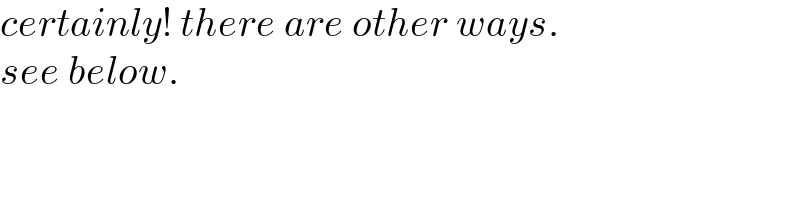
$${certainly}!\:{there}\:{are}\:{other}\:{ways}. \\ $$$${see}\:{below}. \\ $$
Commented by cortano1 last updated on 16/Sep/22
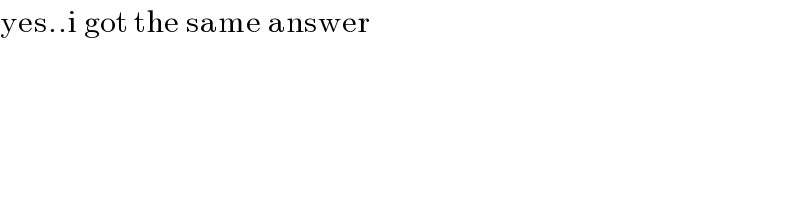
$$\mathrm{yes}..\mathrm{i}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer} \\ $$
Answered by mr W last updated on 16/Sep/22
![(2+(x^2 /4))^5 (1−4x)^5 =2^5 (1+(x^2 /8))^5 (1−4x)^5 =2^5 [Σ_(k=0) ^5 C_k ^5 ((x^2 /8))^k ][Σ_(r=0) ^5 C_r ^5 (−4x)^r ] =2^5 [Σ_(k=0) ^5 C_k ^5 ×(x^(2k) /8^k )][Σ_(r=0) ^5 C_r ^5 (−4)^r x^r ] to get x^2 term: 2k+r=2 ⇒k=0, r=2 or ⇒k=1, r=0 coef. of x^2 term is then: 2^5 ((C_0 ^5 /8^0 )×C_2 ^5 ×(−4)^2 +(C_1 ^5 /8^1 )×C_0 ^5 ×(−4)^0 ) =2^5 ×((1285)/8) =5140](https://www.tinkutara.com/question/Q176341.png)
$$\left(\mathrm{2}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)^{\mathrm{5}} \left(\mathrm{1}−\mathrm{4}{x}\right)^{\mathrm{5}} \\ $$$$=\mathrm{2}^{\mathrm{5}} \left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{8}}\right)^{\mathrm{5}} \left(\mathrm{1}−\mathrm{4}{x}\right)^{\mathrm{5}} \\ $$$$=\mathrm{2}^{\mathrm{5}} \left[\underset{{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{{k}} ^{\mathrm{5}} \left(\frac{{x}^{\mathrm{2}} }{\mathrm{8}}\right)^{{k}} \right]\left[\underset{{r}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{{r}} ^{\mathrm{5}} \left(−\mathrm{4}{x}\right)^{{r}} \right] \\ $$$$=\mathrm{2}^{\mathrm{5}} \left[\underset{{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{{k}} ^{\mathrm{5}} ×\frac{{x}^{\mathrm{2}{k}} }{\mathrm{8}^{{k}} }\right]\left[\underset{{r}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{{r}} ^{\mathrm{5}} \left(−\mathrm{4}\right)^{{r}} {x}^{{r}} \right] \\ $$$${to}\:{get}\:{x}^{\mathrm{2}} \:{term}:\:\mathrm{2}{k}+{r}=\mathrm{2} \\ $$$$\Rightarrow{k}=\mathrm{0},\:{r}=\mathrm{2}\:{or} \\ $$$$\Rightarrow{k}=\mathrm{1},\:{r}=\mathrm{0} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2}} \:{term}\:{is}\:{then}: \\ $$$$\mathrm{2}^{\mathrm{5}} \left(\frac{{C}_{\mathrm{0}} ^{\mathrm{5}} }{\mathrm{8}^{\mathrm{0}} }×{C}_{\mathrm{2}} ^{\mathrm{5}} ×\left(−\mathrm{4}\right)^{\mathrm{2}} +\frac{{C}_{\mathrm{1}} ^{\mathrm{5}} }{\mathrm{8}^{\mathrm{1}} }×{C}_{\mathrm{0}} ^{\mathrm{5}} ×\left(−\mathrm{4}\right)^{\mathrm{0}} \right) \\ $$$$=\mathrm{2}^{\mathrm{5}} ×\frac{\mathrm{1285}}{\mathrm{8}} \\ $$$$=\mathrm{5140} \\ $$
Commented by Ari last updated on 16/Sep/22

$${Thanks}\:{sir}! \\ $$
Commented by mr W last updated on 16/Sep/22
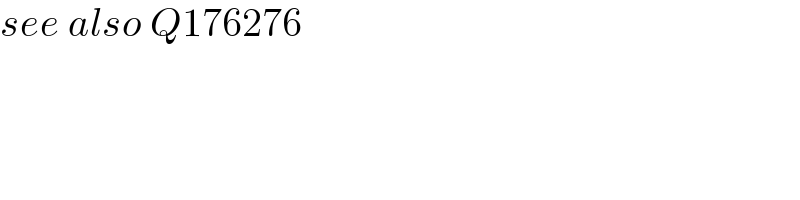
$${see}\:{also}\:{Q}\mathrm{176276} \\ $$
Commented by cortano1 last updated on 16/Sep/22

$$\mathrm{yes}…\mathrm{my}\:\mathrm{way}\:\mathrm{like}\:\mathrm{this} \\ $$
Commented by Tawa11 last updated on 18/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
