Question Number 149469 by mathdanisur last updated on 05/Aug/21
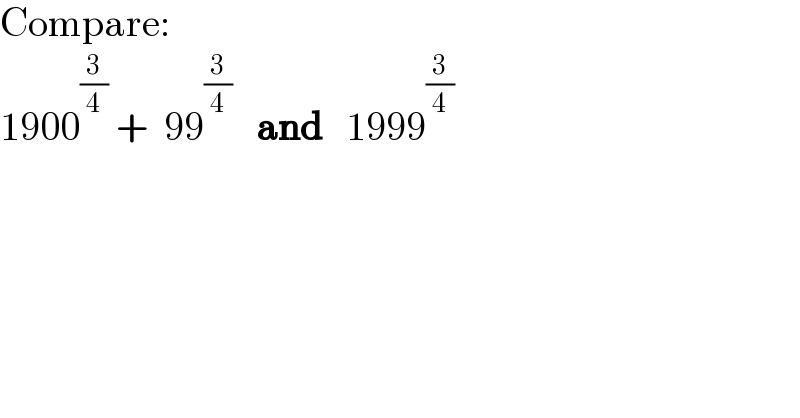
$$\mathrm{Compare}: \\ $$$$\mathrm{1900}^{\frac{\mathrm{3}}{\mathrm{4}}} \:+\:\:\mathrm{99}^{\frac{\mathrm{3}}{\mathrm{4}}} \:\:\:\boldsymbol{\mathrm{and}}\:\:\:\mathrm{1999}^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$
Answered by mindispower last updated on 05/Aug/21
,1[ f′<0 f(1)=f(0)=1 ⇒∀x∈[0,1] f(x)≥1 for x=((1900)/(1999)) f(((1900)/(1999)))=(((1900)/(1999)))^(3/4) +(1−((1900)/(1999)))^(3/4) ≥1 ⇒(1900)^(3/4) +99^(3/4) ≥1999^(3/4)](https://www.tinkutara.com/question/Q149473.png)
$${f}\left({x}\right)={x}^{\frac{\mathrm{3}}{\mathrm{4}}} +\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} ,{x}\in\left[\mathrm{0},\mathrm{1}\left[,{f}\left(\mathrm{1}−{x}\right)={f}\left({x}\right)\right.\right. \\ $$$${f}'\left({x}\right)=\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }−\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\right)=\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{\left({x}\left(\mathrm{1}−{x}\right)\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\right) \\ $$$${if}\:{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}},{f}'>\mathrm{0} \\ $$$$\left.{if}\:{x}\in\right]\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\left[\:{f}'<\mathrm{0}\right. \\ $$$${f}\left(\mathrm{1}\right)={f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\Rightarrow\forall{x}\in\left[\mathrm{0},\mathrm{1}\right]\:\:{f}\left({x}\right)\geqslant\mathrm{1} \\ $$$${for}\:{x}=\frac{\mathrm{1900}}{\mathrm{1999}} \\ $$$${f}\left(\frac{\mathrm{1900}}{\mathrm{1999}}\right)=\left(\frac{\mathrm{1900}}{\mathrm{1999}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} +\left(\mathrm{1}−\frac{\mathrm{1900}}{\mathrm{1999}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \geqslant\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1900}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} +\mathrm{99}^{\frac{\mathrm{3}}{\mathrm{4}}} \geqslant\mathrm{1999}^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 05/Aug/21
$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{Ser}}\:\mathrm{Cool} \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\boldsymbol{\mathrm{Ser}},\:\mathrm{can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as}\:\mathrm{Newton}'\mathrm{s}\: \\ $$$$\mathrm{Binomial}\:\mathrm{or}\:\mathrm{inequality}.? \\ $$
