Question Number 151549 by mathdanisur last updated on 21/Aug/21
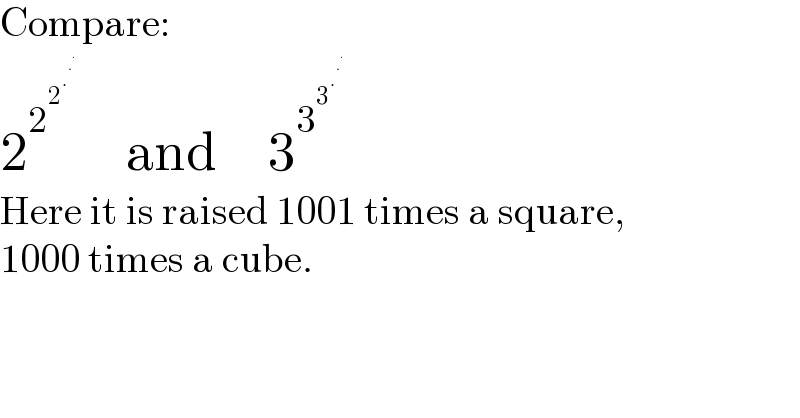
$$\mathrm{Compare}: \\ $$$$\mathrm{2}^{\mathrm{2}^{\mathrm{2}^{.^{.^{.} } } } } \:\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{.^{.^{.} } } } } \\ $$$$\mathrm{Here}\:\mathrm{it}\:\mathrm{is}\:\mathrm{raised}\:\mathrm{1001}\:\mathrm{times}\:\mathrm{a}\:\mathrm{square}, \\ $$$$\mathrm{1000}\:\mathrm{times}\:\mathrm{a}\:\mathrm{cube}. \\ $$
Answered by MJS_new last updated on 21/Aug/21

$${x}^{{x}^{{x}} } ={x}^{\left({x}^{{x}} \right)} \\ $$$$\mathrm{2}^{\left(\mathrm{2}^{\mathrm{2}} \right)} <\mathrm{3}^{\mathrm{3}} \\ $$$${a}<{b} \\ $$$$\mathrm{2}^{{a}} <\mathrm{3}^{{b}} \:\forall\mathrm{0}<{a}\leqslant{b} \\ $$
