Question Number 150603 by mathdanisur last updated on 13/Aug/21
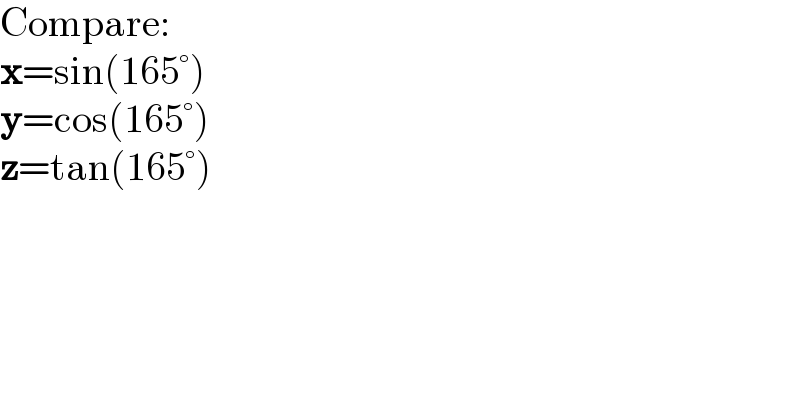
$$\mathrm{Compare}: \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{sin}\left(\mathrm{165}°\right) \\ $$$$\boldsymbol{\mathrm{y}}=\mathrm{cos}\left(\mathrm{165}°\right) \\ $$$$\boldsymbol{\mathrm{z}}=\mathrm{tan}\left(\mathrm{165}°\right) \\ $$
Answered by ajfour last updated on 13/Aug/21
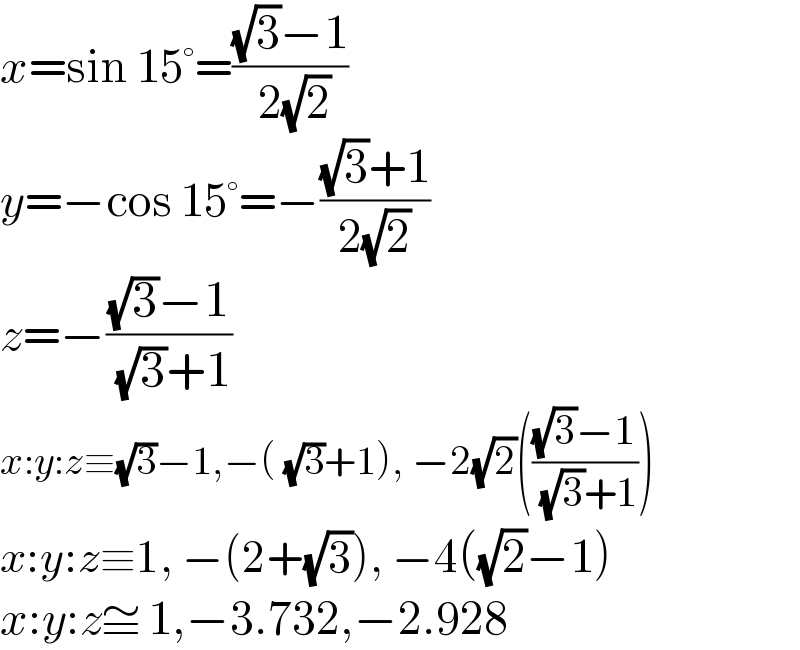
$${x}=\mathrm{sin}\:\mathrm{15}°=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${y}=−\mathrm{cos}\:\mathrm{15}°=−\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${z}=−\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}} \\ $$$${x}:{y}:{z}\equiv\sqrt{\mathrm{3}}−\mathrm{1},−\left(\:\sqrt{\mathrm{3}}+\mathrm{1}\right),\:−\mathrm{2}\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right) \\ $$$${x}:{y}:{z}\equiv\mathrm{1},\:−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right),\:−\mathrm{4}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$${x}:{y}:{z}\cong\:\mathrm{1},−\mathrm{3}.\mathrm{732},−\mathrm{2}.\mathrm{928} \\ $$
Commented by mathdanisur last updated on 14/Aug/21

$$\mathrm{Thankyou}\:\mathrm{Ser} \\ $$
