Question Number 144682 by mathdanisur last updated on 27/Jun/21
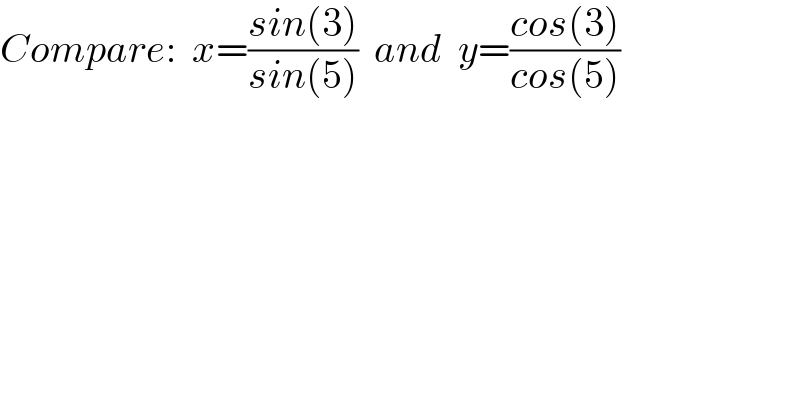
$${Compare}:\:\:{x}=\frac{{sin}\left(\mathrm{3}\right)}{{sin}\left(\mathrm{5}\right)}\:\:{and}\:\:{y}=\frac{{cos}\left(\mathrm{3}\right)}{{cos}\left(\mathrm{5}\right)} \\ $$
Answered by mindispower last updated on 27/Jun/21
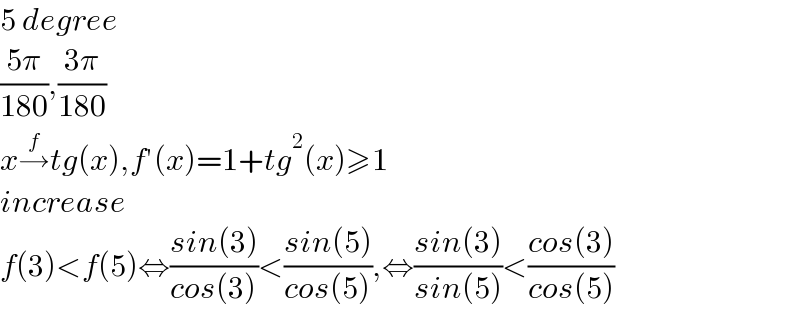
$$\mathrm{5}\:{degree} \\ $$$$\frac{\mathrm{5}\pi}{\mathrm{180}},\frac{\mathrm{3}\pi}{\mathrm{180}} \\ $$$${x}\overset{{f}} {\rightarrow}{tg}\left({x}\right),{f}'\left({x}\right)=\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\geqslant\mathrm{1} \\ $$$${increase}\: \\ $$$${f}\left(\mathrm{3}\right)<{f}\left(\mathrm{5}\right)\Leftrightarrow\frac{{sin}\left(\mathrm{3}\right)}{{cos}\left(\mathrm{3}\right)}<\frac{{sin}\left(\mathrm{5}\right)}{{cos}\left(\mathrm{5}\right)},\Leftrightarrow\frac{{sin}\left(\mathrm{3}\right)}{{sin}\left(\mathrm{5}\right)}<\frac{{cos}\left(\mathrm{3}\right)}{{cos}\left(\mathrm{5}\right)} \\ $$
Commented by mathdanisur last updated on 27/Jun/21
$${perfect}\:{Sir}\:{thanks} \\ $$
