Compute-cos-12-

Question Number 111391 by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Compute}\:\mathrm{cos}\frac{\Pi}{\mathrm{12}} \\ $$

Answered by bemath last updated on 03/Sep/20

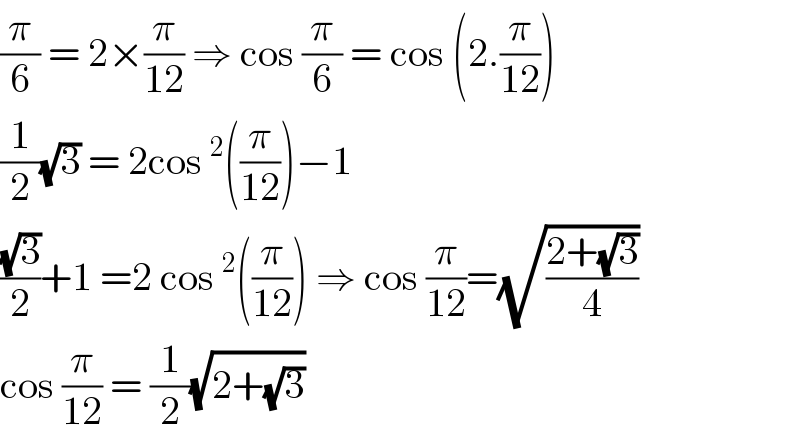
(π/6) = 2×(π/(12)) ⇒ cos (π/6) = cos (2.(π/(12))) (1/2)(√3) = 2cos^2 ((π/(12)))−1 ((√3)/2)+1 =2 cos^2 ((π/(12))) ⇒ cos (π/(12))=(√((2+(√3))/4)) cos (π/(12)) = (1/2)(√(2+(√3)))

$$\frac{\pi}{\mathrm{6}}\:=\:\mathrm{2}×\frac{\pi}{\mathrm{12}}\:\Rightarrow\:\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:=\:\mathrm{cos}\:\left(\mathrm{2}.\frac{\pi}{\mathrm{12}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:=\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)−\mathrm{1} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1}\:=\mathrm{2}\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{12}}\right)\:\Rightarrow\:\mathrm{cos}\:\frac{\pi}{\mathrm{12}}=\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{4}}} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$

Commented by bemath last updated on 03/Sep/20

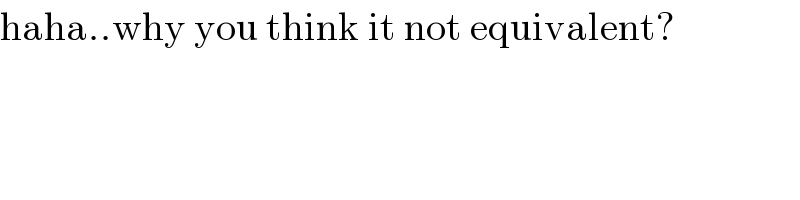
$$\mathrm{haha}..\mathrm{why}\:\mathrm{you}\:\mathrm{think}\:\mathrm{it}\:\mathrm{not}\:\mathrm{equivalent}? \\ $$

Commented by bemath last updated on 03/Sep/20

Commented by bemath last updated on 03/Sep/20

$$\mathrm{look}\:\mathrm{it}\: \\ $$

Commented by bobhans last updated on 03/Sep/20

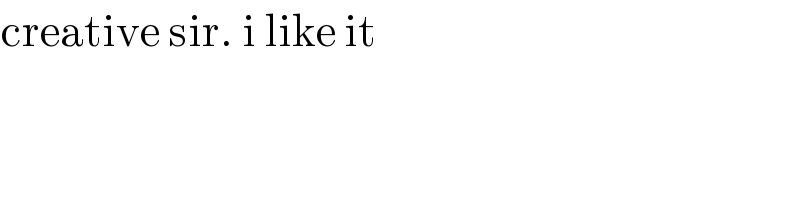
$$\mathrm{creative}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{like}\:\mathrm{it} \\ $$

Answered by ajfour last updated on 03/Sep/20

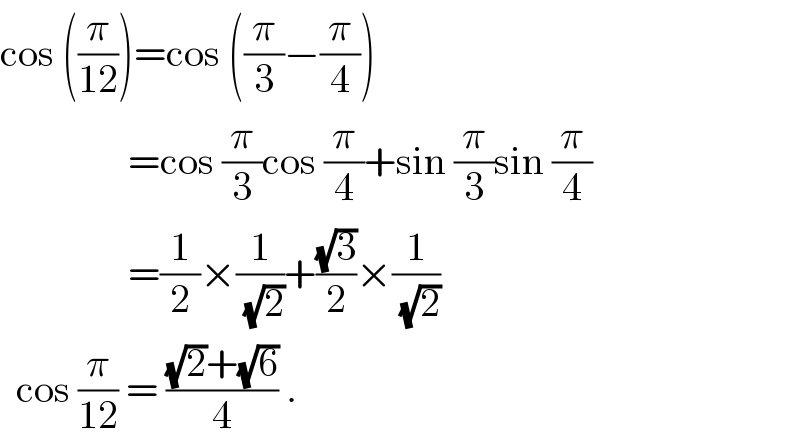
cos ((π/(12)))=cos ((π/3)−(π/4)) =cos (π/3)cos (π/4)+sin (π/3)sin (π/4) =(1/2)×(1/( (√2)))+((√3)/2)×(1/( (√2))) cos (π/(12)) = (((√2)+(√6))/4) .

$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{12}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\mathrm{sin}\:\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\mathrm{cos}\:\frac{\pi}{\mathrm{12}}\:=\:\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{4}}\:. \\ $$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Thanks}. \\ $$

Commented by bemath last updated on 03/Sep/20

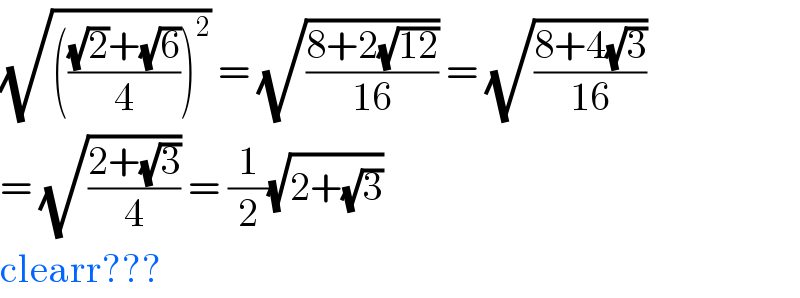
(√(((((√2)+(√6))/4))^2 )) = (√((8+2(√(12)))/(16))) = (√((8+4(√3))/(16))) = (√((2+(√3))/4)) = (1/2)(√(2+(√3))) clearr???

$$\sqrt{\left(\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\:\sqrt{\frac{\mathrm{8}+\mathrm{2}\sqrt{\mathrm{12}}}{\mathrm{16}}}\:=\:\sqrt{\frac{\mathrm{8}+\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{16}}} \\ $$$$=\:\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{4}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{clearr}??? \\ $$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Yes}.\:\mathrm{Thanks}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply