Question Number 17102 by tawa tawa last updated on 30/Jun/17
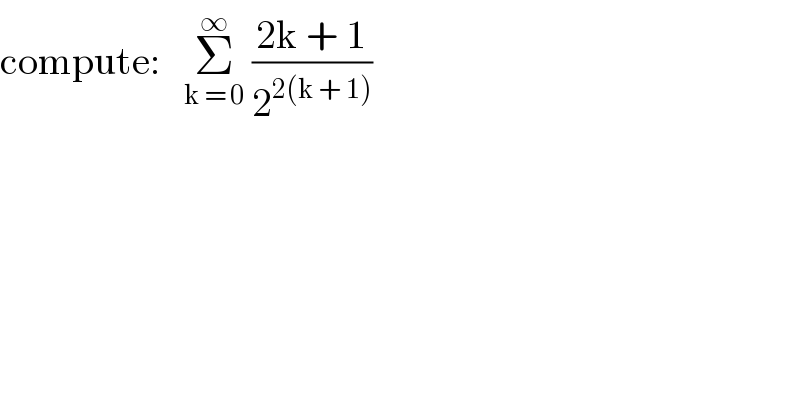
$$\mathrm{compute}:\:\:\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2k}\:+\:\mathrm{1}}{\mathrm{2}^{\mathrm{2}\left(\mathrm{k}\:+\:\mathrm{1}\right)} } \\ $$
Commented by prakash jain last updated on 01/Jul/17
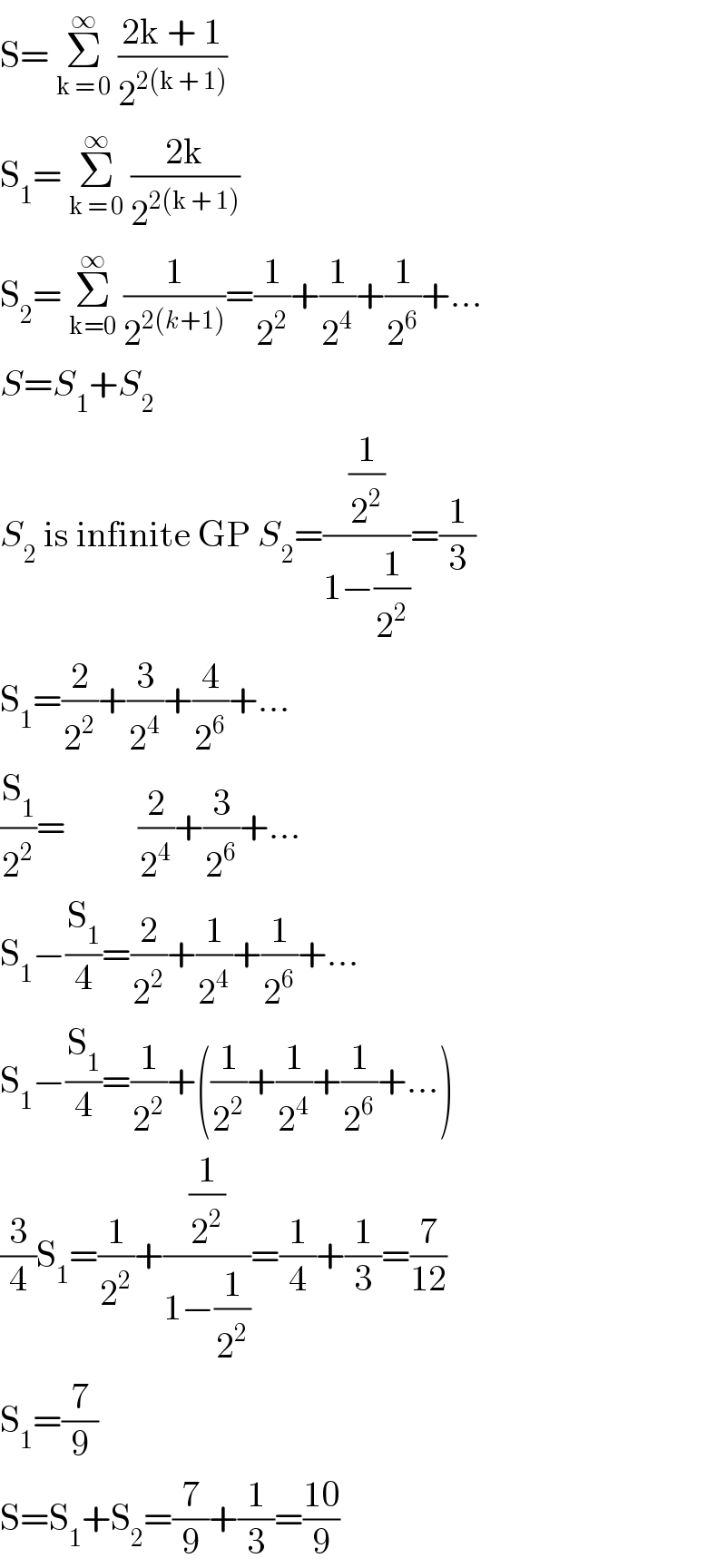
$$\mathrm{S}=\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2k}\:+\:\mathrm{1}}{\mathrm{2}^{\mathrm{2}\left(\mathrm{k}\:+\:\mathrm{1}\right)} } \\ $$$$\mathrm{S}_{\mathrm{1}} =\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2k}}{\mathrm{2}^{\mathrm{2}\left(\mathrm{k}\:+\:\mathrm{1}\right)} } \\ $$$$\mathrm{S}_{\mathrm{2}} =\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}\left({k}+\mathrm{1}\right)} }=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }+… \\ $$$${S}={S}_{\mathrm{1}} +{S}_{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{infinite}\:\mathrm{GP}\:{S}_{\mathrm{2}} =\frac{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{S}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{6}} }+… \\ $$$$\frac{\mathrm{S}_{\mathrm{1}} }{\mathrm{2}^{\mathrm{2}} }=\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{6}} }+… \\ $$$$\mathrm{S}_{\mathrm{1}} −\frac{\mathrm{S}_{\mathrm{1}} }{\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }+… \\ $$$$\mathrm{S}_{\mathrm{1}} −\frac{\mathrm{S}_{\mathrm{1}} }{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }+…\right) \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{12}} \\ $$$$\mathrm{S}_{\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{9}} \\ $$$$\mathrm{S}=\mathrm{S}_{\mathrm{1}} +\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{9}} \\ $$
Commented by ajfour last updated on 01/Jul/17
$$\mathrm{utter}\:\mathrm{simple}\:\mathrm{for}\:\mathrm{you}\:\mathrm{Sir}. \\ $$
Commented by tawa tawa last updated on 01/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
