Question Number 117973 by bemath last updated on 14/Oct/20
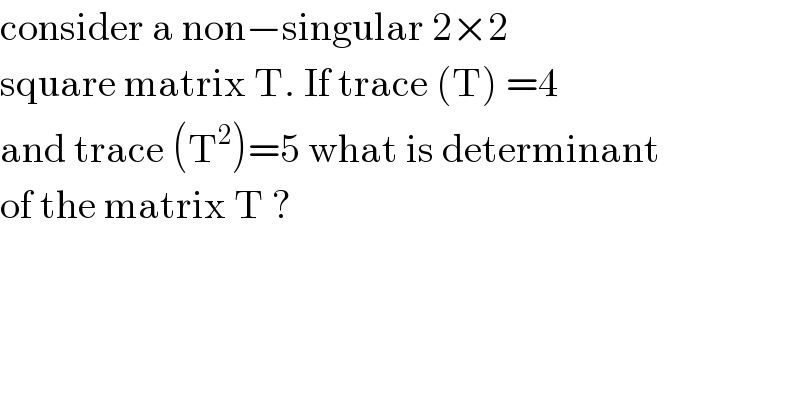
$$\mathrm{consider}\:\mathrm{a}\:\mathrm{non}−\mathrm{singular}\:\mathrm{2}×\mathrm{2}\: \\ $$$$\mathrm{square}\:\mathrm{matrix}\:\mathrm{T}.\:\mathrm{If}\:\mathrm{trace}\:\left(\mathrm{T}\right)\:=\mathrm{4} \\ $$$$\mathrm{and}\:\mathrm{trace}\:\left(\mathrm{T}^{\mathrm{2}} \right)=\mathrm{5}\:\mathrm{what}\:\mathrm{is}\:\mathrm{determinant} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{matrix}\:\mathrm{T}\:? \\ $$
Answered by bobhans last updated on 14/Oct/20
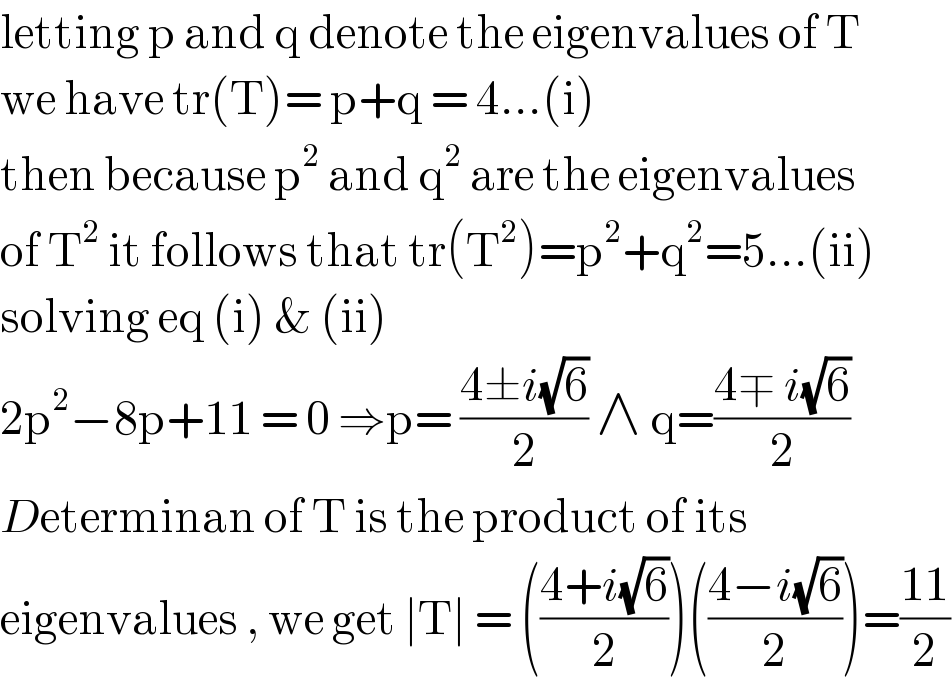
$$\mathrm{letting}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{denote}\:\mathrm{the}\:\mathrm{eigenvalues}\:\mathrm{of}\:\mathrm{T} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{tr}\left(\mathrm{T}\right)=\:\mathrm{p}+\mathrm{q}\:=\:\mathrm{4}…\left(\mathrm{i}\right) \\ $$$$\mathrm{then}\:\mathrm{because}\:\mathrm{p}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{q}^{\mathrm{2}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{eigenvalues} \\ $$$$\mathrm{of}\:\mathrm{T}^{\mathrm{2}} \:\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{tr}\left(\mathrm{T}^{\mathrm{2}} \right)=\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{5}…\left(\mathrm{ii}\right) \\ $$$$\mathrm{solving}\:\mathrm{eq}\:\left(\mathrm{i}\right)\:\&\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{2p}^{\mathrm{2}} −\mathrm{8p}+\mathrm{11}\:=\:\mathrm{0}\:\Rightarrow\mathrm{p}=\:\frac{\mathrm{4}\pm{i}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\wedge\:\mathrm{q}=\frac{\mathrm{4}\mp\:{i}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${D}\mathrm{eterminan}\:\mathrm{of}\:\mathrm{T}\:\mathrm{is}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{its} \\ $$$$\mathrm{eigenvalues}\:,\:\mathrm{we}\:\mathrm{get}\:\mid\mathrm{T}\mid\:=\:\left(\frac{\mathrm{4}+{i}\sqrt{\mathrm{6}}}{\mathrm{2}}\right)\left(\frac{\mathrm{4}−{i}\sqrt{\mathrm{6}}}{\mathrm{2}}\right)=\frac{\mathrm{11}}{\mathrm{2}} \\ $$
