Question Number 113865 by Ar Brandon last updated on 15/Sep/20
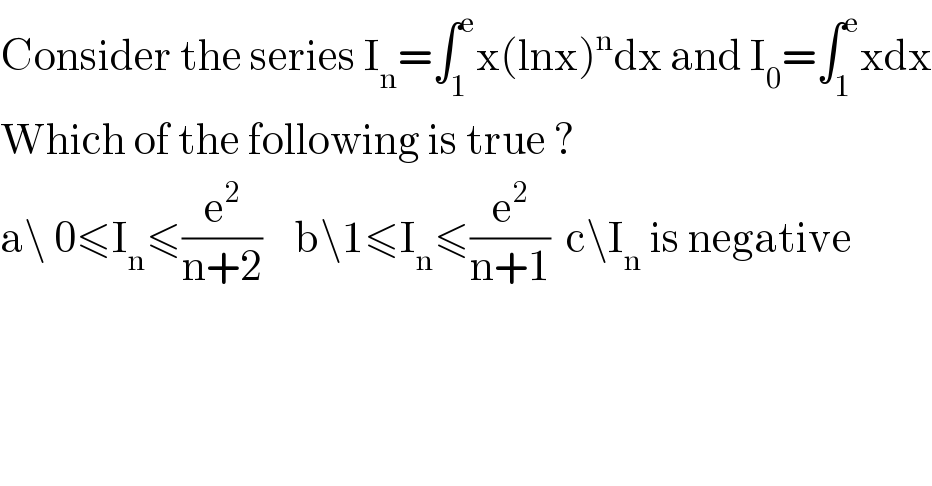
$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{series}\:\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{1}} ^{\mathrm{e}} \mathrm{x}\left(\mathrm{lnx}\right)^{\mathrm{n}} \mathrm{dx}\:\mathrm{and}\:\mathrm{I}_{\mathrm{0}} =\int_{\mathrm{1}} ^{\mathrm{e}} \mathrm{xdx} \\ $$$$\mathrm{Which}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{is}\:\mathrm{true}\:? \\ $$$$\mathrm{a}\backslash\:\mathrm{0}\leqslant\mathrm{I}_{\mathrm{n}} \leqslant\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{n}+\mathrm{2}}\:\:\:\:\mathrm{b}\backslash\mathrm{1}\leqslant\mathrm{I}_{\mathrm{n}} \leqslant\frac{\mathrm{e}^{\mathrm{2}} }{\mathrm{n}+\mathrm{1}}\:\:\mathrm{c}\backslash\mathrm{I}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{negative} \\ $$
