Consider-the-system-shown-in-the-figure-Initially-the-system-was-in-rest-i-Find-the-acceleration-of-block-if-man-climbs-the-rod-with-acceleration-a-w-r-t-rod-ii-If-the-man-climb-to-the-top-of

Question Number 23224 by Tinkutara last updated on 27/Oct/17

Consider the system shown in the

figure . Initially the system was in rest .

(i) Find the acceleration of block if man

climbs the rod with acceleration a (w . r . t .

rod)

(ii) If the man climb to the top of the

rod then find the distance moved by the

block .

Commented by mrW1 last updated on 27/Oct/17

(1)

let a_{R} = acceleration of rod (↑) and block (↓)

a_{M} = acceleration of man (↑)

a_{M} = a + a_{R}

F = force between rod and man

F - mg = {ma}_{M} = m (a + a_{R})

\Rightarrow F = m (g + a + a_{R})

(M + m - M) g - F = (M + m + M) a_{R}

(M + m - M) g - m (g + a + a_{R}) = (M + m + M) a_{R}

- ma = 2 (M + m) a_{R}

\Rightarrow a_{R} = - \frac{ma}{2 (M + m)}

(2)

L = \frac{1}{2} {at}^{2}

Δ H = \frac{1}{2} a_{R} t^{2}

\Rightarrow Δ H = \frac{a_{R}}{a} \times L

\Rightarrow Δ H = - \frac{m}{2 (M + m)} \times L

(the block moves up a distance \frac{mL}{2 (M + m)})

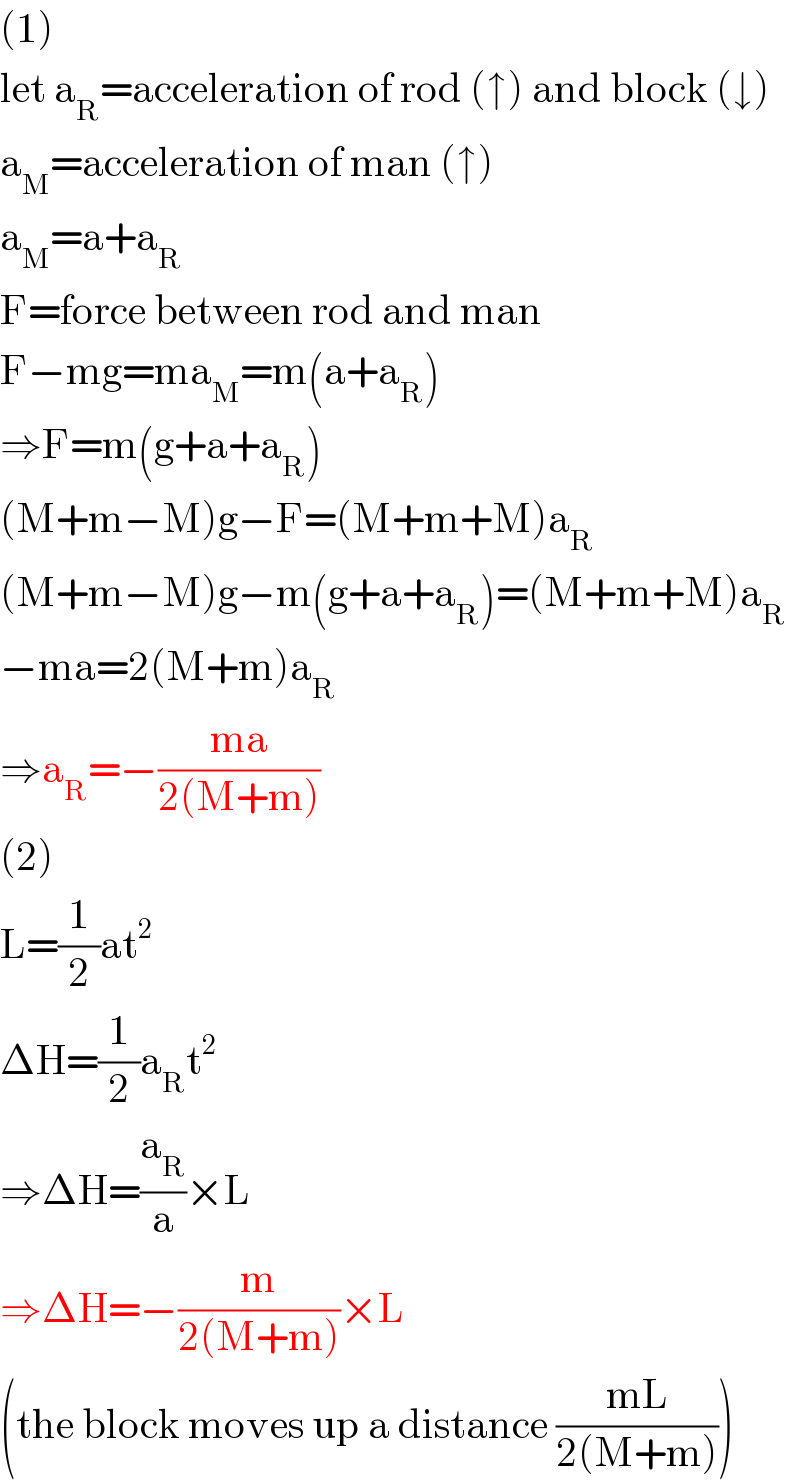
Commented by Tinkutara last updated on 27/Oct/17

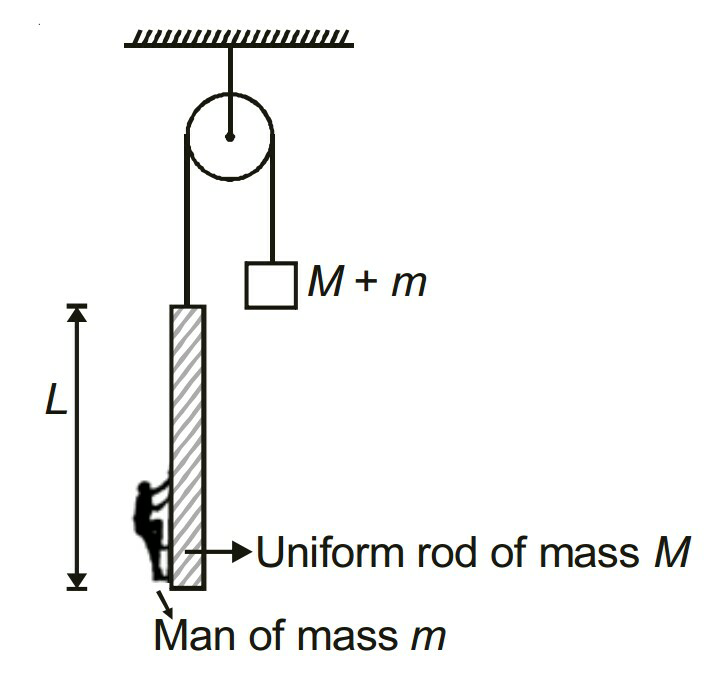
Commented by mrW1 last updated on 27/Oct/17

that depents on which direction is

defined as positive . in your book the

+ ve direction for the block is upwards,

so there is no “ -^{″} . i defined + ve direction

downwards, so i have “ -^{″} . the result

is the same, i . e . the block moves a

distance \frac{mL}{2 (M + m)} upwards .

Commented by Tinkutara last updated on 28/Oct/17

OK Thanks .