Question Number 61840 by psyche last updated on 10/Jun/19

$$\boldsymbol{{consider}}\:\boldsymbol{{the}}\:\boldsymbol{{triple}}\:\boldsymbol{{of}}\:\boldsymbol{{real}}\:\boldsymbol{{numbers}}\:\left(\boldsymbol{{x}},{y},{z}\right) \\ $$$${defined}\:{by}\:{the}\:{addittion}\:\left(\boldsymbol{{x}},{y},{z}\right)+\left({x}',{y}',{z}'\right)=\left({x}+{x}',{y}+{y}',{z}+{z}'\right) \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{scalar}}\:\boldsymbol{{multiplication}}\:\boldsymbol{{by}}\:\:\:\boldsymbol{\alpha}\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right).\: \\ $$$$\boldsymbol{{S}}{how}\:{that}\:{all}\:{axioms}\:{for}\:{a}\:{vector}\:{space}\:{are}\:{satisfied}\:{except}\:{axiom}\:\mathrm{8}. \\ $$
Answered by arcana last updated on 10/Jun/19
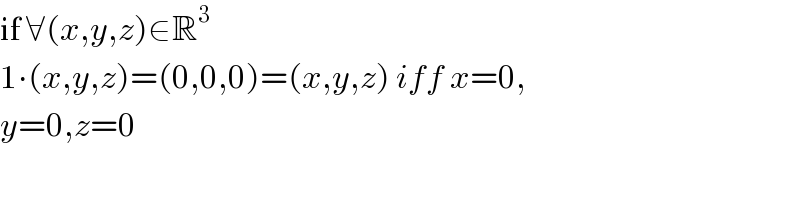
$$\mathrm{if}\:\forall\left({x},{y},{z}\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$$\mathrm{1}\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)=\left({x},{y},{z}\right)\:{iff}\:{x}=\mathrm{0}, \\ $$$${y}=\mathrm{0},{z}=\mathrm{0} \\ $$$$ \\ $$
Commented by psyche last updated on 10/Jun/19
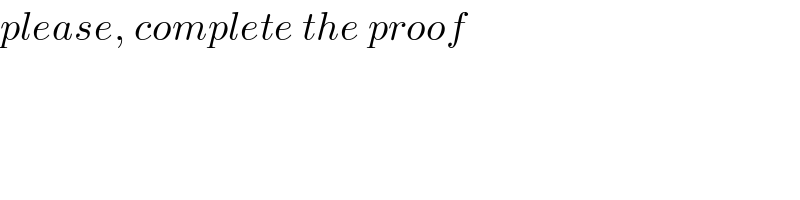
$${please},\:{complete}\:{the}\:{proof} \\ $$
Commented by arcana last updated on 10/Jun/19
![axiom 1,2,3,4 define (R^3 ,“+”) is a structure of group with sum usual in R^3 we need a field K because define ∙ operation. elements in K are scalars, elements inR^3 are vectors if R=K (field) ∙:R×R^3 →R^3 (α,a)→α∙a axiom5 α,β∈R,(x,y,z)∈R^3 α+β∈R ⇒(α+β)∙(x,y,z)=(0,0,0) def. “∙” β∙(x,y,z)=(0,0,0) ; β∙(x,y,z)=(0,0,0) ⇒(α+β)∙(x,y,z)=α∙(x,y,z)+β∙(x,y,z) axiom 6 α∈R,(x,y,z),(x′,y′,z′)∈R^3 α∙[(x,y,z)+(x′,y′,z′)]=α∙(x+x′,y+y′,z+z′) (x+x′,y+y′,z+z′)∈R^3 ⇒α∙(x+x′,y+y′,z+z′)=(0,0,0) α∙[(x,y,z)+(x′,y′,z′)]α∙(x,y,z)=(0,0,0) ; α∙(x′,y′,z′)=(0,0,0) ⇒α∙[(x,y,z)+(x′,y′,z′)]=α∙(x,y,z)+α∙(x′,y′,z′) axiom 7 α,β∈R,(x,y,z)∈R^3 .αβ∈R (αβ)∙(x,y,z)=(0,0,0) β∙(x,y,z)=(0,0,0) ⇒α∙[β∙(x,y,z)]=α∙(0,0,0)=(0,0,0) ⇒(αβ)∙(x,y,z)=α∙[β∙(x,y,z)]](https://www.tinkutara.com/question/Q61851.png)
$$\mathrm{axiom}\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:\mathrm{define}\:\left(\mathbb{R}^{\mathrm{3}} ,“+''\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{structure}\:\mathrm{of}\:\mathrm{group} \\ $$$$\mathrm{with}\:\mathrm{sum}\:\mathrm{usual}\:\mathrm{in}\:\mathbb{R}^{\mathrm{3}} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{a}\:\mathrm{field}\:\mathrm{K}\:\mathrm{because}\:\mathrm{define}\:\centerdot\:\mathrm{operation}. \\ $$$$\mathrm{elements}\:\mathrm{in}\:\mathrm{K}\:\mathrm{are}\:\mathrm{scalars},\:\mathrm{elements}\:\mathrm{in}\mathbb{R}^{\mathrm{3}} \:\mathrm{are}\:\mathrm{vectors} \\ $$$$\mathrm{if}\:\mathbb{R}=\mathrm{K}\:\left(\mathrm{field}\right) \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\centerdot:\mathbb{R}×\mathbb{R}^{\mathrm{3}} \rightarrow\mathbb{R}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\alpha,{a}\right)\rightarrow\alpha\centerdot{a} \\ $$$$\mathrm{axiom5} \\ $$$$\alpha,\beta\in\mathbb{R},\left({x},{y},{z}\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$$\alpha+\beta\in\mathbb{R} \\ $$$$\Rightarrow\left(\alpha+\beta\right)\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:\mathrm{def}.\:“\centerdot'' \\ $$$$\beta\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:;\:\beta\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$ \\ $$$$\Rightarrow\left(\alpha+\beta\right)\centerdot\left({x},{y},{z}\right)=\alpha\centerdot\left({x},{y},{z}\right)+\beta\centerdot\left({x},{y},{z}\right) \\ $$$$ \\ $$$$\mathrm{axiom}\:\mathrm{6} \\ $$$$\alpha\in\mathbb{R},\left({x},{y},{z}\right),\left({x}',{y}',{z}'\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$$\alpha\centerdot\left[\left({x},{y},{z}\right)+\left({x}',{y}',{z}'\right)\right]=\alpha\centerdot\left({x}+{x}',{y}+{y}',{z}+{z}'\right) \\ $$$$\left({x}+{x}',{y}+{y}',{z}+{z}'\right)\in\mathbb{R}^{\mathrm{3}} \\ $$$$ \\ $$$$\Rightarrow\alpha\centerdot\left({x}+{x}',{y}+{y}',{z}+{z}'\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$\alpha\centerdot\left[\left({x},{y},{z}\right)+\left({x}',{y}',{z}'\right)\right]\alpha\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:;\:\alpha\centerdot\left({x}',{y}',{z}'\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$ \\ $$$$\Rightarrow\alpha\centerdot\left[\left({x},{y},{z}\right)+\left({x}',{y}',{z}'\right)\right]=\alpha\centerdot\left({x},{y},{z}\right)+\alpha\centerdot\left({x}',{y}',{z}'\right) \\ $$$$ \\ $$$$\mathrm{axiom}\:\mathrm{7} \\ $$$$\alpha,\beta\in\mathbb{R},\left({x},{y},{z}\right)\in\mathbb{R}^{\mathrm{3}} .\alpha\beta\in\mathbb{R} \\ $$$$\left(\alpha\beta\right)\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$\beta\centerdot\left({x},{y},{z}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:\Rightarrow\alpha\centerdot\left[\beta\centerdot\left({x},{y},{z}\right)\right]=\alpha\centerdot\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$$ \\ $$$$\Rightarrow\left(\alpha\beta\right)\centerdot\left({x},{y},{z}\right)=\alpha\centerdot\left[\beta\centerdot\left({x},{y},{z}\right)\right] \\ $$$$ \\ $$
