Question Number 43135 by MrW3 last updated on 07/Sep/18

$${Construct}\:{a}\:{triangle}\:\Delta{ABC}\:{with} \\ $$$$\angle{B}=\mathrm{50}° \\ $$$${AC}=\mathrm{6}\:{cm} \\ $$$${AB}+{BC}=\mathrm{8}\:{cm} \\ $$$$ \\ $$$${see}\:{also}\:{Q}\mathrm{42942}. \\ $$
Commented by math1967 last updated on 08/Sep/18

Commented by math1967 last updated on 08/Sep/18
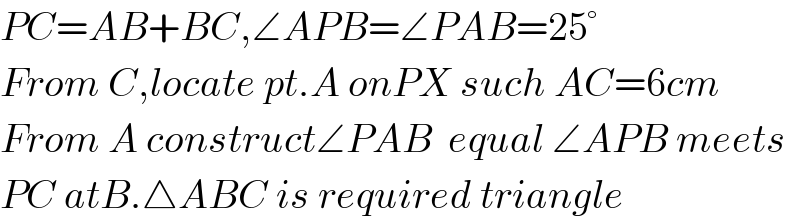
$${PC}={AB}+{BC},\angle{APB}=\angle{PAB}=\mathrm{25}° \\ $$$${From}\:{C},{locate}\:{pt}.{A}\:{onPX}\:{such}\:{AC}=\mathrm{6}{cm} \\ $$$${From}\:{A}\:{construct}\angle{PAB}\:\:{equal}\:\angle{APB}\:{meets} \\ $$$${PC}\:{atB}.\bigtriangleup{ABC}\:{is}\:{required}\:{triangle} \\ $$
Commented by MrW3 last updated on 08/Sep/18

$${Very}\:{nice},\:{thank}\:{you}\:{sir}! \\ $$
Commented by math1967 last updated on 08/Sep/18
$${You}\:{are}\:{welcome}\:{sir} \\ $$
Answered by behi83417@gmail.com last updated on 07/Sep/18
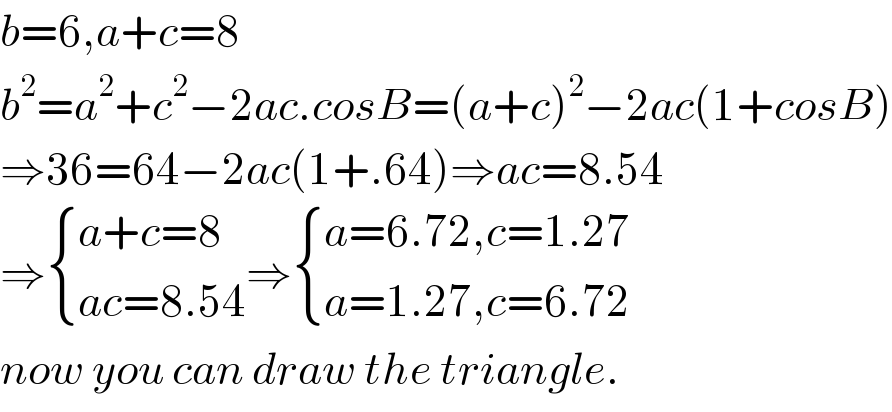
$${b}=\mathrm{6},{a}+{c}=\mathrm{8} \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}.{cosB}=\left({a}+{c}\right)^{\mathrm{2}} −\mathrm{2}{ac}\left(\mathrm{1}+{cosB}\right) \\ $$$$\Rightarrow\mathrm{36}=\mathrm{64}−\mathrm{2}{ac}\left(\mathrm{1}+.\mathrm{64}\right)\Rightarrow{ac}=\mathrm{8}.\mathrm{54} \\ $$$$\Rightarrow\begin{cases}{{a}+{c}=\mathrm{8}}\\{{ac}=\mathrm{8}.\mathrm{54}}\end{cases}\Rightarrow\begin{cases}{{a}=\mathrm{6}.\mathrm{72},{c}=\mathrm{1}.\mathrm{27}}\\{{a}=\mathrm{1}.\mathrm{27},{c}=\mathrm{6}.\mathrm{72}}\end{cases} \\ $$$${now}\:{you}\:{can}\:{draw}\:{the}\:{triangle}. \\ $$
Commented by MrW3 last updated on 07/Sep/18
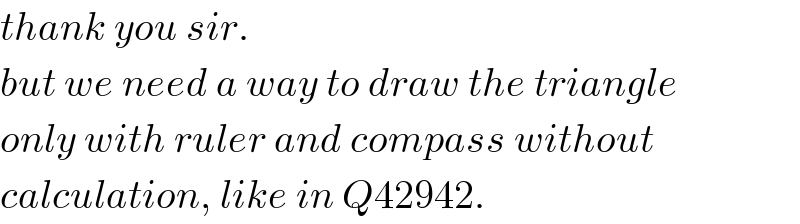
$${thank}\:{you}\:{sir}. \\ $$$${but}\:{we}\:{need}\:{a}\:{way}\:{to}\:{draw}\:{the}\:{triangle} \\ $$$${only}\:{with}\:{ruler}\:{and}\:{compass}\:{without} \\ $$$${calculation},\:{like}\:{in}\:{Q}\mathrm{42942}. \\ $$
