Menu Close

Convergence-of-1-I-1-e-t-5-sin-lnt-t-1-3-2-dt-2-I-1-lnx-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 79325 by Henri Boucatchou last updated on 24/Jan/20
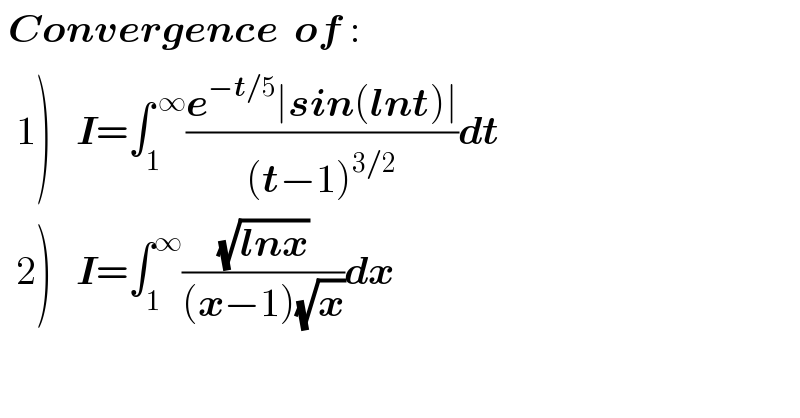
Convergence of : 1) I=∫_1 ^( ∞) ((e^(−t/5) ∣sin(lnt)∣)/((t−1)^(3/2) ))dt 2) I=∫_1 ^∞ ((√(lnx))/((x−1)(√x)))dx
$$\:\boldsymbol{{Convergence}}\:\:\boldsymbol{{of}}\:: \\ $$$$\left.\:\:\mathrm{1}\right)\:\:\:\boldsymbol{{I}}=\int_{\mathrm{1}} ^{\:\infty} \frac{\boldsymbol{{e}}^{−\boldsymbol{{t}}/\mathrm{5}} \mid\boldsymbol{{sin}}\left(\boldsymbol{{lnt}}\right)\mid}{\left(\boldsymbol{{t}}−\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }\boldsymbol{{dt}} \\ $$$$\left.\:\:\mathrm{2}\right)\:\:\:\boldsymbol{{I}}=\int_{\mathrm{1}} ^{\infty} \frac{\sqrt{\boldsymbol{{lnx}}}}{\left(\boldsymbol{{x}}−\mathrm{1}\right)\sqrt{\boldsymbol{{x}}}}\boldsymbol{{dx}} \\ $$
Commented by mathmax by abdo last updated on 24/Jan/20
1) changement t−1 =x give I =∫_1 ^(+∞) ((e^(−(t/5)) ∣sin(lnt)∣)/((t−1)^(3/2) ))dt =∫_0 ^∞ ((e^(−((1+x)/5)) ∣sin(ln(1+x)∣)/x^(3/2) )dx=∫_0 ^∞ ϕ(x)dx I =∫_0 ^1 (...)dx +∫_1 ^(+∞) (...)dx at V(0) ∣sin(ln(1+x)∣∼∣sin(x)∣∼∣x∣ ⇒ ϕ(x) ∼ ((e^(−(1/5)) x)/x^(3/2) ) =(e^(−(1/5)) /x^(1/2) ) and ∫_0 ^1 e^(−(1/5)) x^(−(1/2)) dx converges at +∞ ∣ϕ(x)∣ ≤(e^(−((1+x)/5)) /x^(3/2) ) ⇒∫_1 ^(+∞) ∣ϕ(x)∣dx ≤∫_1 ^(+∞) x^(−(3/2)) e^(−((1+x)/5)) dx we have lim x^2 x^(−(3/2)) e^(−((1+x)/5)) =0 ⇒this integral converges ⇒ I converges
$$\left.\mathrm{1}\right)\:{changement}\:{t}−\mathrm{1}\:={x}\:{give} \\ $$$${I}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{{e}^{−\frac{{t}}{\mathrm{5}}} \mid{sin}\left({lnt}\right)\mid}{\left({t}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\frac{\mathrm{1}+{x}}{\mathrm{5}}} \mid{sin}\left({ln}\left(\mathrm{1}+{x}\right)\mid\right.}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}=\int_{\mathrm{0}} ^{\infty} \:\varphi\left({x}\right){dx} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(…\right){dx}\:+\int_{\mathrm{1}} ^{+\infty} \left(…\right){dx}\:\:{at}\:{V}\left(\mathrm{0}\right)\:\:\:\mid{sin}\left({ln}\left(\mathrm{1}+{x}\right)\mid\sim\mid{sin}\left({x}\right)\mid\sim\mid{x}\mid\right. \\ $$$$\Rightarrow\:\varphi\left({x}\right)\:\sim\:\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{5}}} {x}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\frac{{e}^{−\frac{\mathrm{1}}{\mathrm{5}}} }{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }\:\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−\frac{\mathrm{1}}{\mathrm{5}}} \:{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{dx}\:{converges} \\ $$$${at}\:+\infty\:\:\mid\varphi\left({x}\right)\mid\:\leqslant\frac{{e}^{−\frac{\mathrm{1}+{x}}{\mathrm{5}}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \mid\varphi\left({x}\right)\mid{dx}\:\leqslant\int_{\mathrm{1}} ^{+\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−\frac{\mathrm{1}+{x}}{\mathrm{5}}} \:{dx} \\ $$$${we}\:{have}\:{lim}\:{x}^{\mathrm{2}} \:{x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−\frac{\mathrm{1}+{x}}{\mathrm{5}}} =\mathrm{0}\:\Rightarrow{this}\:{integral}\:{converges}\:\Rightarrow \\ $$$${I}\:{converges} \\ $$
Commented by mathmax by abdo last updated on 24/Jan/20
2) I =∫_1 ^(+∞) ((√(lnx))/((x−1)(√x)))dx changement (√(lnx))=t give lnx =t^2 ⇒ x =e^t^2 ⇒ I =∫_0 ^∞ (t/((e^t^2 −1)e^(t^2 /2) )) ×2t e^t^2 dt =∫_0 ^∞ ((2t^2 e^(t^2 /2) )/(e^t^2 −1))dt =_ ∫_0 ^∞ ((2t^2 e^(−t^2 ) e^(t^2 /2) )/(1−e^(−t^2 ) ))dt =∫_0 ^∞ ((2t^2 e^(−(t^2 /2)) )/(1−e^(−t^2 ) ))dt =∫_0 ^1 (...)dt + ∫_1 ^(+∞) (...)dt at V(0) e^(−t^2 ) ∼1−t^2 ⇒1−e^(−t^2 ) ∼1−1+t^2 ⇒ ⇒((2t^2 e^(−(t^2 /2)) )/(1−e^(−t^2 ) )) ∼2e^(−(t^2 /2)) →2 (t→0) ⇒∫_0 ^1 ((2t e^(−(t^2 /2)) )/(1−e^(−t^2 ) ))dt converges let ξ>0 we have lim_(t→+∞) t^(1+ξ) ×((2t e^(−(t^2 /2)) )/(1−e^(−t^2 ) )) =0 ⇒∫_1 ^(+∞) ((2t^2 e^(−(t^2 /2)) )/(1−e^(−t^2 ) )) converges finally I is convergent
$$\left.\mathrm{2}\right)\:\:{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\sqrt{{lnx}}}{\left({x}−\mathrm{1}\right)\sqrt{{x}}}{dx}\:\:{changement}\:\sqrt{{lnx}}={t}\:{give}\:{lnx}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}\:={e}^{{t}^{\mathrm{2}} } \:\:\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{t}}{\left({e}^{{t}^{\mathrm{2}} } −\mathrm{1}\right){e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }\:×\mathrm{2}{t}\:{e}^{{t}^{\mathrm{2}} } {dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:{e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{{e}^{{t}^{\mathrm{2}} } −\mathrm{1}}{dt} \\ $$$$=_{} \int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{t}^{\mathrm{2}} {e}^{−{t}^{\mathrm{2}} } \:{e}^{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(…\right){dt}\:+\:\int_{\mathrm{1}} ^{+\infty} \:\left(…\right){dt} \\ $$$${at}\:{V}\left(\mathrm{0}\right)\:{e}^{−{t}^{\mathrm{2}} } \sim\mathrm{1}−{t}^{\mathrm{2}} \:\Rightarrow\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } \sim\mathrm{1}−\mathrm{1}+{t}^{\mathrm{2}} \Rightarrow\:\Rightarrow\frac{\mathrm{2}{t}^{\mathrm{2}} \:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }\:\sim\mathrm{2}{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} \:\rightarrow\mathrm{2}\:\left({t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{t}\:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }{dt}\:{converges}\:\:{let}\:\xi>\mathrm{0}\:{we}\:{have} \\ $$$${lim}_{{t}\rightarrow+\infty} \:\:{t}^{\mathrm{1}+\xi} \:\:×\frac{\mathrm{2}{t}\:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }\:=\mathrm{0}\:\Rightarrow\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{2}{t}^{\mathrm{2}} \:{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{1}−{e}^{−{t}^{\mathrm{2}} } }\:{converges} \\ $$$${finally}\:{I}\:{is}\:{convergent} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *