Menu Close

convergence-radius-of-n-N-2-n-z-n-

Tinku Tara 0 Comments
Pin




Question Number 99496 by ~blr237~ last updated on 21/Jun/20
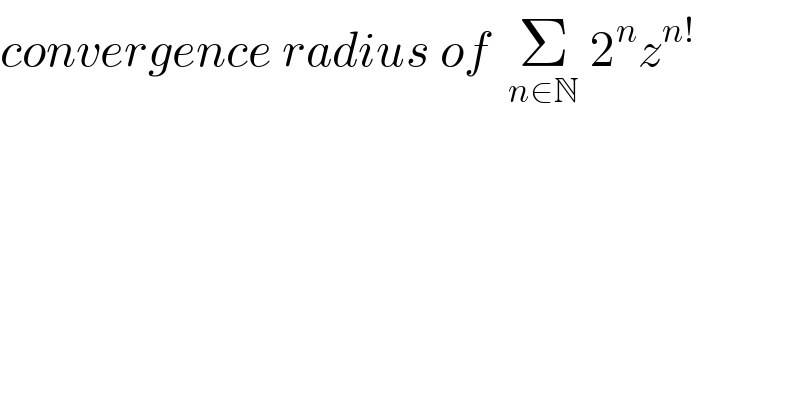
convergence radius of Σ_(n∈N) 2^n z^(n!)
$${convergence}\:{radius}\:{of}\:\:\underset{{n}\in\mathbb{N}} {\sum}\:\mathrm{2}^{{n}} {z}^{{n}!} \: \\ $$
Answered by mathmax by abdo last updated on 21/Jun/20
u_n =2^n z^(n!) is with positive terms (u_(n+1) /u_n ) =((2^(n+1) z^((n+1)!) )/(2^(n ) z^(n!) )) =2 z^((n+1)!−n!) =2 z^((n+1)n!−n!) =2 z^(n(n!) ) =2 z^(ϕ(n)) (ϕ(n)→∞) if ∣z∣<(1/2)⇒∣2z^(ϕ(n)) ∣<1 and lim_(n→+∞) (u_(n+1) /u_n ) =0 ⇒Σ u_n converges anther wayu_n ^(1/(n )) =2 (z^(n!) )^(1/n) =2( z)^((n−1)!) ⇒if ∣z∣<(1/2) ⇒lim_(n∞) u_n ^(1/n) =0 ⇒Σ u_n converges ⇒r =(1/2)
$$\mathrm{u}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \:\mathrm{z}^{\mathrm{n}!} \:\mathrm{is}\:\mathrm{with}\:\mathrm{positive}\:\mathrm{terms}\: \\ $$$$\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\:=\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:\mathrm{z}^{\left(\mathrm{n}+\mathrm{1}\right)!} }{\mathrm{2}^{\mathrm{n}\:} \mathrm{z}^{\mathrm{n}!} }\:=\mathrm{2}\:\mathrm{z}^{\left(\mathrm{n}+\mathrm{1}\right)!−\mathrm{n}!} \:=\mathrm{2}\:\mathrm{z}^{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}!−\mathrm{n}!} \:=\mathrm{2}\:\mathrm{z}^{\mathrm{n}\left(\mathrm{n}!\right)\:} \:=\mathrm{2}\:\mathrm{z}^{\varphi\left(\mathrm{n}\right)} \:\:\:\:\:\left(\varphi\left(\mathrm{n}\right)\rightarrow\infty\right) \\ $$$$\mathrm{if}\:\mid\mathrm{z}\mid<\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mid\mathrm{2z}^{\varphi\left(\mathrm{n}\right)} \mid<\mathrm{1}\:\:\mathrm{and}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\:=\mathrm{0}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{converges} \\ $$$$\mathrm{anther}\:\mathrm{wayu}_{\mathrm{n}} ^{\frac{\mathrm{1}}{\mathrm{n}\:}} \:\:=\mathrm{2}\:\left(\mathrm{z}^{\mathrm{n}!} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\mathrm{2}\left(\:\mathrm{z}\right)^{\left(\mathrm{n}−\mathrm{1}\right)!} \:\:\Rightarrow\mathrm{if}\:\mid\mathrm{z}\mid<\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\infty} \:\:\mathrm{u}_{\mathrm{n}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\mathrm{0}\:\Rightarrow\Sigma\:\mathrm{u}_{\mathrm{n}} \:\mathrm{converges} \\ $$$$\Rightarrow\mathrm{r}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by maths mind last updated on 21/Jun/20
sir i think R=1 Σ2^n ((2/3))^(n!) ∃a<1 &∃N∈N ∣ ∀n≥N 2^n ((2/3))^(n!) <a^n ⇔n!ln((2/3))<nln((a/2)) ⇔(n−1)!≥((ln((a/2)))/(ln((2/3)))),a=(1/4) (n−1)!≥((ln(8))/(ln((3/2)))) hase solution since (n−1)!→∞ Σ2^n ((2/3))^(n!) =Σ_(n=0) ^(N−1) 2^n ((2/3))^(n!) +Σ_(k≥N) 2^k ((2/3))^k first finit sum 2nd 2^k ((2/3))^k <((1/4))^n by comparaison Cv let a<1 ∃N_a ∈N∣∀n≥N 2^n (aaaa)^(n!) <((a/2))^n ⇔n!ln(a)<nln((a/4))⇔(n−1)!>((ln((a/4)))/(ln(a))) hase always solution for a∈]0,1[
$$\:{sir}\:{i}\:{think}\:{R}=\mathrm{1} \\ $$$$\Sigma\mathrm{2}^{{n}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}!} \\ $$$$\exists{a}<\mathrm{1}\:\&\exists{N}\in\mathbb{N}\:\mid\:\forall{n}\geqslant{N}\: \\ $$$$\mathrm{2}^{{n}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}!} <{a}^{{n}} \\ $$$$\Leftrightarrow{n}!{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)<{nln}\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Leftrightarrow\left({n}−\mathrm{1}\right)!\geqslant\frac{{ln}\left(\frac{{a}}{\mathrm{2}}\right)}{{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)},{a}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({n}−\mathrm{1}\right)!\geqslant\frac{{ln}\left(\mathrm{8}\right)}{{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}\:\:\:{hase}\:{solution}\:{since}\:\left({n}−\mathrm{1}\right)!\rightarrow\infty \\ $$$$\Sigma\mathrm{2}^{{n}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}!} =\underset{{n}=\mathrm{0}} {\overset{{N}−\mathrm{1}} {\sum}}\mathrm{2}^{{n}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}!} +\underset{{k}\geqslant{N}} {\sum}\mathrm{2}^{{k}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{k}} \\ $$$${first}\:{finit}\:{sum}\:\mathrm{2}{nd} \\ $$$$\mathrm{2}^{{k}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{k}} <\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \:\:{by}\:{comparaison}\:{Cv} \\ $$$${let}\:{a}<\mathrm{1}\: \\ $$$$\exists{N}_{{a}} \in\mathbb{N}\mid\forall{n}\geqslant{N}\:\mathrm{2}^{{n}} \left({aaaa}\right)^{{n}!} <\left(\frac{{a}}{\mathrm{2}}\right)^{{n}} \\ $$$$\Leftrightarrow{n}!{ln}\left({a}\right)<{nln}\left(\frac{{a}}{\mathrm{4}}\right)\Leftrightarrow\left({n}−\mathrm{1}\right)!>\frac{{ln}\left(\frac{{a}}{\mathrm{4}}\right)}{{ln}\left({a}\right)}\:{hase}\:{always}\:{solution} \\ $$$$\left.{for}\:{a}\in\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$
Commented by mathmax by abdo last updated on 22/Jun/20
perhaps sir i am not sure for my answer because this serie is more complicated with this factoriel..!
$$\mathrm{perhaps}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{am}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{for}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{because}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{more} \\ $$$$\mathrm{complicated}\:\mathrm{with}\:\mathrm{this}\:\mathrm{factoriel}..! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *