cos-1-2-pix-2-dx-

Question Number 117438 by hatakekakashi1729gmailcom last updated on 11/Oct/20

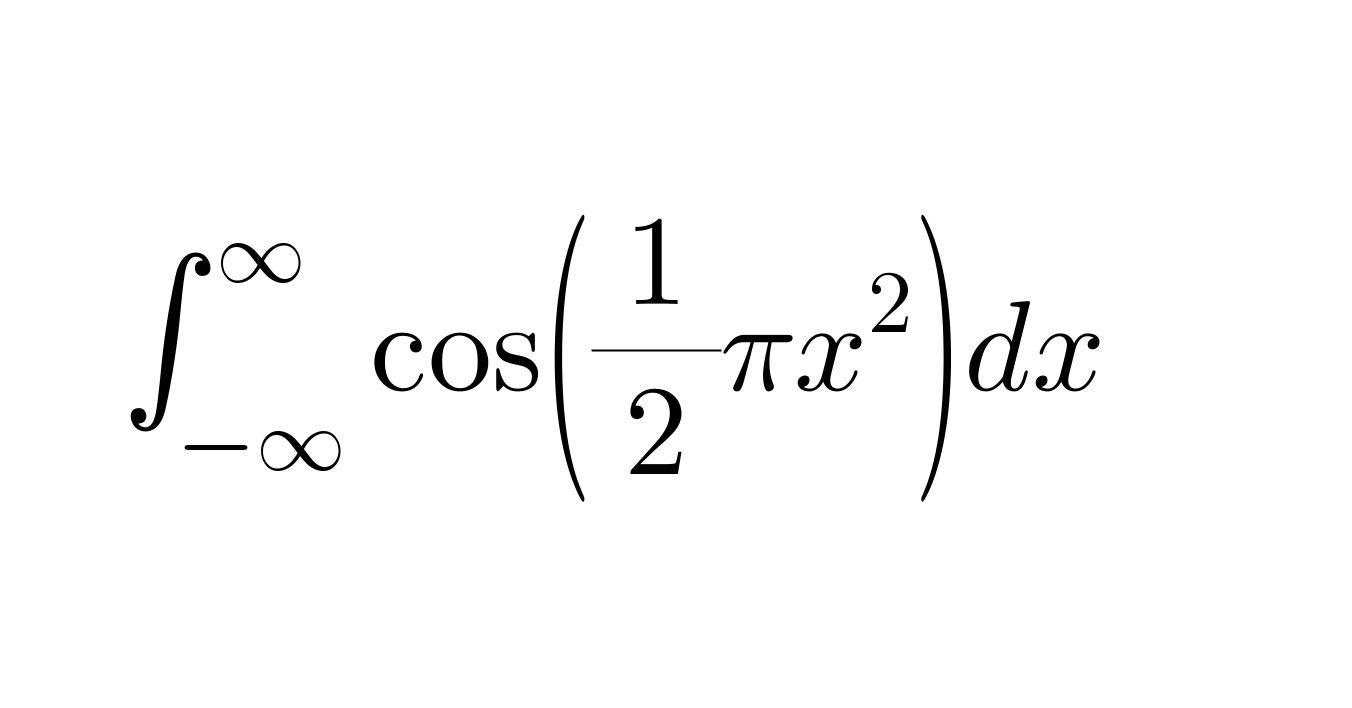
$$ \\ $$$$\:\:\:\:\:\int_{−\infty} ^{\:\infty} \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi{x}^{\mathrm{2}} \right){dx}\:\:\:\:\: \\ $$$$ \\ $$

Answered by AbduraufKodiriy last updated on 11/Oct/20

Answered by AbduraufKodiriy last updated on 11/Oct/20

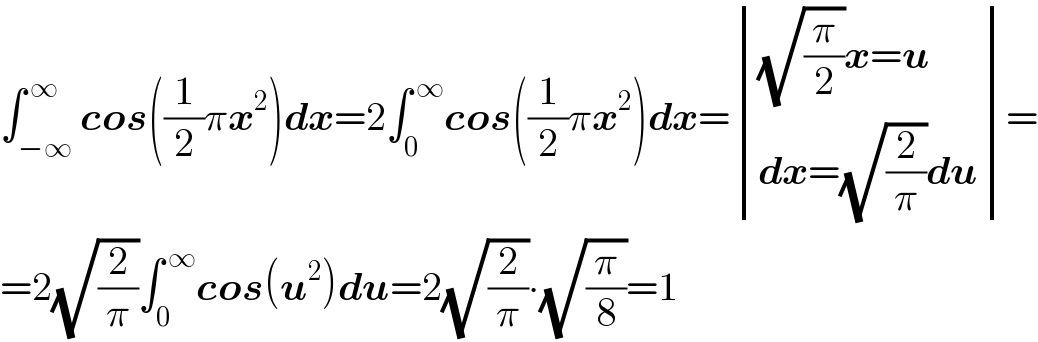
∫_(−∞) ^( ∞) cos((1/2)πx^2 )dx=2∫_0 ^( ∞) cos((1/2)πx^2 )dx= determinant ((((√(π/2))x=u)),((dx=(√(2/π))du)))= =2(√(2/π))∫_0 ^( ∞) cos(u^2 )du=2(√(2/π))∙(√(π/8))=1

$$\int_{−\infty} ^{\:\infty} \boldsymbol{{cos}}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi\boldsymbol{{x}}^{\mathrm{2}} \right)\boldsymbol{{dx}}=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \boldsymbol{{cos}}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi\boldsymbol{{x}}^{\mathrm{2}} \right)\boldsymbol{{dx}}=\begin{vmatrix}{\sqrt{\frac{\pi}{\mathrm{2}}}\boldsymbol{{x}}=\boldsymbol{{u}}}\\{\boldsymbol{{dx}}=\sqrt{\frac{\mathrm{2}}{\pi}}\boldsymbol{{du}}}\end{vmatrix}= \\ $$$$=\mathrm{2}\sqrt{\frac{\mathrm{2}}{\pi}}\int_{\mathrm{0}} ^{\:\infty} \boldsymbol{{cos}}\left(\boldsymbol{{u}}^{\mathrm{2}} \right)\boldsymbol{{du}}=\mathrm{2}\sqrt{\frac{\mathrm{2}}{\pi}}\centerdot\sqrt{\frac{\pi}{\mathrm{8}}}=\mathrm{1} \\ $$

Answered by AbduraufKodiriy last updated on 11/Oct/20

Answered by mathmax by abdo last updated on 11/Oct/20

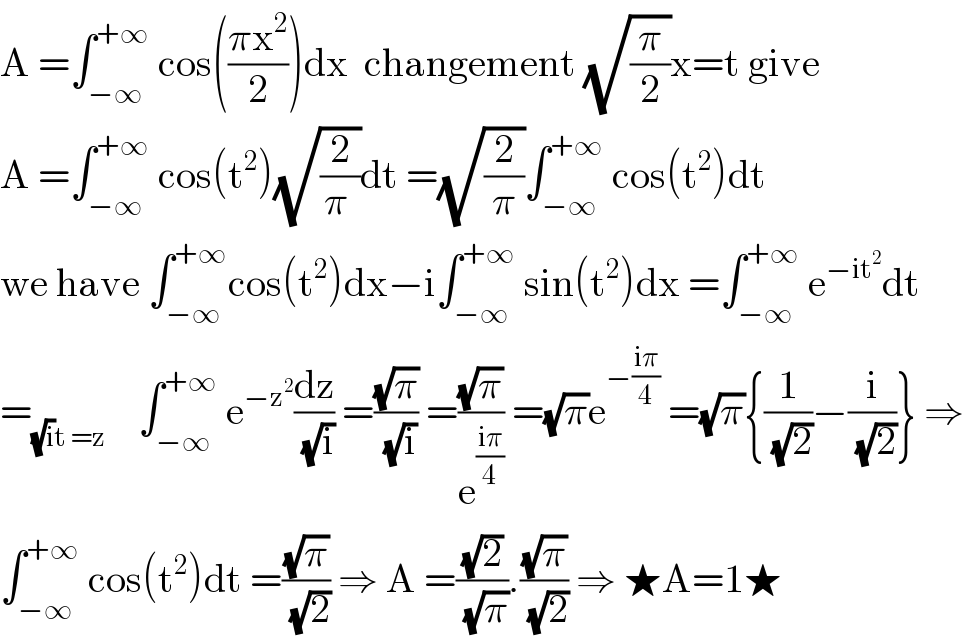
A =∫_(−∞) ^(+∞) cos(((πx^2 )/2))dx changement (√(π/2))x=t give A =∫_(−∞) ^(+∞) cos(t^2 )(√(2/(π )))dt =(√(2/π))∫_(−∞) ^(+∞) cos(t^2 )dt we have ∫_(−∞) ^(+∞) cos(t^2 )dx−i∫_(−∞) ^(+∞) sin(t^2 )dx =∫_(−∞) ^(+∞) e^(−it^2 ) dt =_((√i)t =z) ∫_(−∞) ^(+∞) e^(−z^2 ) (dz/( (√i))) =((√π)/( (√i))) =((√π)/e^((iπ)/4) ) =(√π)e^(−((iπ)/4)) =(√π){(1/( (√2)))−(i/( (√2)))} ⇒ ∫_(−∞) ^(+∞) cos(t^2 )dt =((√π)/( (√2))) ⇒ A =((√2)/( (√π))).((√π)/( (√2))) ⇒ ★A=1★

$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\mathrm{cos}\left(\frac{\pi\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\frac{\pi}{\mathrm{2}}}\mathrm{x}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\sqrt{\frac{\mathrm{2}}{\pi\:}}\mathrm{dt}\:=\sqrt{\frac{\mathrm{2}}{\pi}}\int_{−\infty} ^{+\infty} \:\mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{−\infty} ^{+\infty} \mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dx}−\mathrm{i}\int_{−\infty} ^{+\infty} \:\mathrm{sin}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{it}^{\mathrm{2}} } \mathrm{dt} \\ $$$$=_{\sqrt{\mathrm{i}}\mathrm{t}\:=\mathrm{z}} \:\:\:\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\:\sqrt{\mathrm{i}}}\:=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{i}}}\:=\frac{\sqrt{\pi}}{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\:=\sqrt{\pi}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:=\sqrt{\pi}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right\}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}\:=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:\mathrm{A}\:=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\pi}}.\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:\bigstar\mathrm{A}=\mathrm{1}\bigstar \\ $$

Commented by AbduraufKodiriy last updated on 11/Oct/20

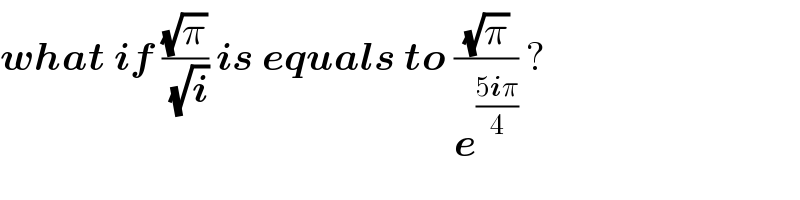
what if ((√π)/( (√i))) is equals to ((√π)/e^((5iπ)/4) ) ?

$$\boldsymbol{{what}}\:\boldsymbol{{if}}\:\frac{\sqrt{\pi}}{\:\sqrt{\boldsymbol{{i}}}}\:\boldsymbol{{is}}\:\boldsymbol{{equals}}\:\boldsymbol{{to}}\:\frac{\sqrt{\pi}}{\boldsymbol{{e}}^{\frac{\mathrm{5}\boldsymbol{{i}}\pi}{\mathrm{4}}} }\:? \\ $$

Commented by Bird last updated on 12/Oct/20

we take the principal value of e^z and lnz (principal determinatin)

$${we}\:{take}\:{the}\:{principal}\:{value}\:{of} \\ $$$${e}^{{z}} \:{and}\:{lnz}\:\:\left({principal}\:{determinatin}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply