cos-1-2x-2-1-2x-2-cos-1-x-2-2-x-2-120-2pi-3-Find-x-

Question Number 61511 by Kunal12588 last updated on 03/Jun/19

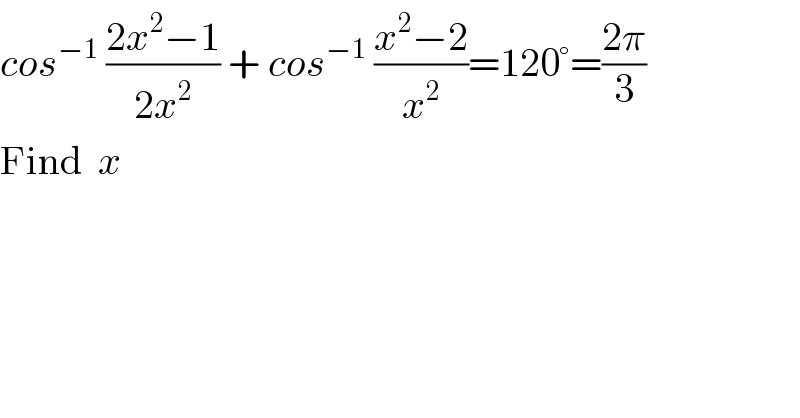
$${cos}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\:{cos}^{−\mathrm{1}} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} }=\mathrm{120}°=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{Find}\:\:{x} \\ $$

Answered by MJS last updated on 03/Jun/19

$$\mathrm{cos}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\mathrm{cos}^{−\mathrm{1}} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\pi−\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\:−\mathrm{sin}^{−\mathrm{1}} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} }=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{3}}−\mathrm{sin}^{−\mathrm{1}} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }=−\frac{{x}^{\mathrm{2}} −\mathrm{2}−\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}{x}^{\mathrm{2}} }\:\left[\mathrm{beware}\:\mathrm{of}\:\mathrm{false}\:\mathrm{solutions}!!!\right] \\ $$$$\Rightarrow\:{x}=\pm\mathrm{1}\:\left[\mathrm{false}!\right]\:\vee\:{x}=\pm\frac{\sqrt{\mathrm{21}}}{\mathrm{3}} \\ $$

Commented by Kunal12588 last updated on 04/Jun/19

$${thank}\:{you}\:{sir} \\ $$

Commented by Kunal12588 last updated on 04/Jun/19

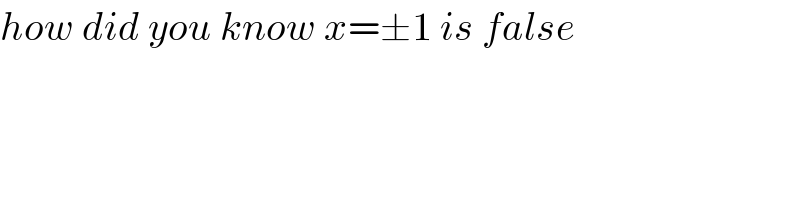
$${how}\:{did}\:{you}\:{know}\:{x}=\pm\mathrm{1}\:{is}\:{false} \\ $$

Commented by Kunal12588 last updated on 04/Jun/19

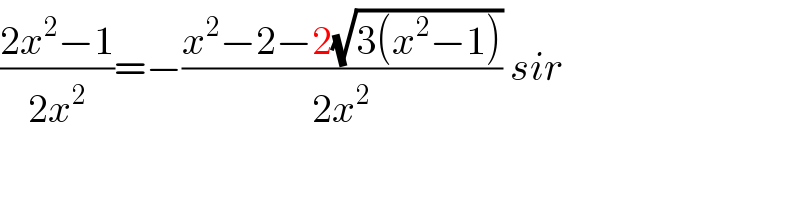
$$\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }=−\frac{{x}^{\mathrm{2}} −\mathrm{2}−\mathrm{2}\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}{x}^{\mathrm{2}} }\:{sir} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com