Menu Close

cos-1-cos-2-cos-3-cos-44-sin-1-sin-2-sin-3-sin-44-

Tinku Tara 0 Comments
Pin




Question Number 127045 by benjo_mathlover last updated on 26/Dec/20
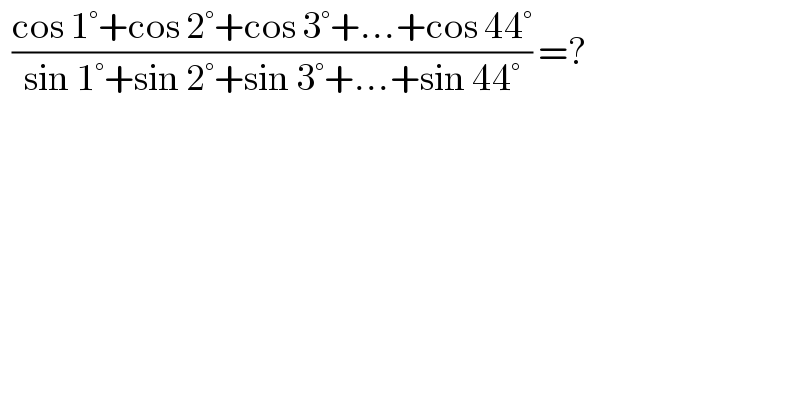
((cos 1°+cos 2°+cos 3°+...+cos 44°)/(sin 1°+sin 2°+sin 3°+...+sin 44°)) =?
$$\:\:\frac{\mathrm{cos}\:\mathrm{1}°+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{3}°+…+\mathrm{cos}\:\mathrm{44}°}{\mathrm{sin}\:\mathrm{1}°+\mathrm{sin}\:\mathrm{2}°+\mathrm{sin}\:\mathrm{3}°+…+\mathrm{sin}\:\mathrm{44}°}\:=? \\ $$
Answered by liberty last updated on 26/Dec/20
((cos (22.5°−21.5°)+cos (22.5°−20.5°)+...+cos(22.5°+20.5°)+cos (22.5°+21.5°) )/(sin (22.5°−21.5°)+sin (22.5°−20.5°)+...+sin (22.5°+20.5°)+sin (22.5+21.5°))) = ((2cos 22.5°cos 21.5°+2cos 22.5°cos 20.5°+...+2cos 22.5°cos 0.5°)/(2sin 22.5°cos 21.5°+2sin 22.5°cos 20.5°+...+2sin 22.5°cos 0.5°)) = ((cos 22.5°(cos 21.5°+cos 20.5°+...+cos 0.5°))/(sin 22.5°(cos 21.5°+cos 20.5°+...+cos 0.5°))) = cot 22.5° = (1/(tan (π/8)))
$$\:\frac{\mathrm{cos}\:\left(\mathrm{22}.\mathrm{5}°−\mathrm{21}.\mathrm{5}°\right)+\mathrm{cos}\:\left(\mathrm{22}.\mathrm{5}°−\mathrm{20}.\mathrm{5}°\right)+…+\mathrm{cos}\left(\mathrm{22}.\mathrm{5}°+\mathrm{20}.\mathrm{5}°\right)+\mathrm{cos}\:\left(\mathrm{22}.\mathrm{5}°+\mathrm{21}.\mathrm{5}°\right)\:}{\mathrm{sin}\:\left(\mathrm{22}.\mathrm{5}°−\mathrm{21}.\mathrm{5}°\right)+\mathrm{sin}\:\left(\mathrm{22}.\mathrm{5}°−\mathrm{20}.\mathrm{5}°\right)+…+\mathrm{sin}\:\left(\mathrm{22}.\mathrm{5}°+\mathrm{20}.\mathrm{5}°\right)+\mathrm{sin}\:\left(\mathrm{22}.\mathrm{5}+\mathrm{21}.\mathrm{5}°\right)}\:= \\ $$$$\frac{\mathrm{2cos}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{21}.\mathrm{5}°+\mathrm{2cos}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{20}.\mathrm{5}°+…+\mathrm{2cos}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{0}.\mathrm{5}°}{\mathrm{2sin}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{21}.\mathrm{5}°+\mathrm{2sin}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{20}.\mathrm{5}°+…+\mathrm{2sin}\:\mathrm{22}.\mathrm{5}°\mathrm{cos}\:\mathrm{0}.\mathrm{5}°}\:= \\ $$$$\frac{\mathrm{cos}\:\mathrm{22}.\mathrm{5}°\left(\mathrm{cos}\:\mathrm{21}.\mathrm{5}°+\mathrm{cos}\:\mathrm{20}.\mathrm{5}°+…+\mathrm{cos}\:\mathrm{0}.\mathrm{5}°\right)}{\mathrm{sin}\:\mathrm{22}.\mathrm{5}°\left(\mathrm{cos}\:\mathrm{21}.\mathrm{5}°+\mathrm{cos}\:\mathrm{20}.\mathrm{5}°+…+\mathrm{cos}\:\mathrm{0}.\mathrm{5}°\right)}\:= \\ $$$$\mathrm{cot}\:\mathrm{22}.\mathrm{5}°\:=\:\frac{\mathrm{1}}{\mathrm{tan}\:\left(\pi/\mathrm{8}\right)} \\ $$
Commented by benjo_mathlover last updated on 26/Dec/20
yes...thanks
$${yes}…{thanks} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Dec/20
((cos1°+cos2°+cos3°+...+cos44°)/(sin1°+sin2°+...+sin44°)) =(((1/(2sin(1/2)°))(sin(3/2)°−sin(1/2)°+sin(5/2)°−sin(3/2)°+sin((89)/2)°−sin((87)/2)°))/((1/(2sin((1°)/2)))(cos(1/2)°−cos(3/2)°+cos(3/2)°−cos(5/2)°+...+cos((87)/2)°−cos((89)/2)°))) =((sin((89)/2)°−sin(1/2)°)/(cos(1/2)°−cos((89)/2)°))=((2cos(π/8)sin(1/2)°)/(2sin(π/8)sin(1/2)°))=(√((2+(√2))/(2−(√2))))=(√2)+1
$$\frac{{cos}\mathrm{1}°+{cos}\mathrm{2}°+{cos}\mathrm{3}°+…+{cos}\mathrm{44}°}{{sin}\mathrm{1}°+{sin}\mathrm{2}°+…+{sin}\mathrm{44}°} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\mathrm{1}}{\mathrm{2}}°}\left({sin}\frac{\mathrm{3}}{\mathrm{2}}°−{sin}\frac{\mathrm{1}}{\mathrm{2}}°+{sin}\frac{\mathrm{5}}{\mathrm{2}}°−{sin}\frac{\mathrm{3}}{\mathrm{2}}°+{sin}\frac{\mathrm{89}}{\mathrm{2}}°−{sin}\frac{\mathrm{87}}{\mathrm{2}}°\right)}{\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\mathrm{1}°}{\mathrm{2}}}\left({cos}\frac{\mathrm{1}}{\mathrm{2}}°−{cos}\frac{\mathrm{3}}{\mathrm{2}}°+{cos}\frac{\mathrm{3}}{\mathrm{2}}°−{cos}\frac{\mathrm{5}}{\mathrm{2}}°+…+{cos}\frac{\mathrm{87}}{\mathrm{2}}°−{cos}\frac{\mathrm{89}}{\mathrm{2}}°\right)} \\ $$$$=\frac{{sin}\frac{\mathrm{89}}{\mathrm{2}}°−{sin}\frac{\mathrm{1}}{\mathrm{2}}°}{{cos}\frac{\mathrm{1}}{\mathrm{2}}°−{cos}\frac{\mathrm{89}}{\mathrm{2}}°}=\frac{\mathrm{2}{cos}\frac{\pi}{\mathrm{8}}{sin}\frac{\mathrm{1}}{\mathrm{2}}°}{\mathrm{2}{sin}\frac{\pi}{\mathrm{8}}{sin}\frac{\mathrm{1}}{\mathrm{2}}°}=\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}}=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *