Question Number 144998 by imjagoll last updated on 01/Jul/21
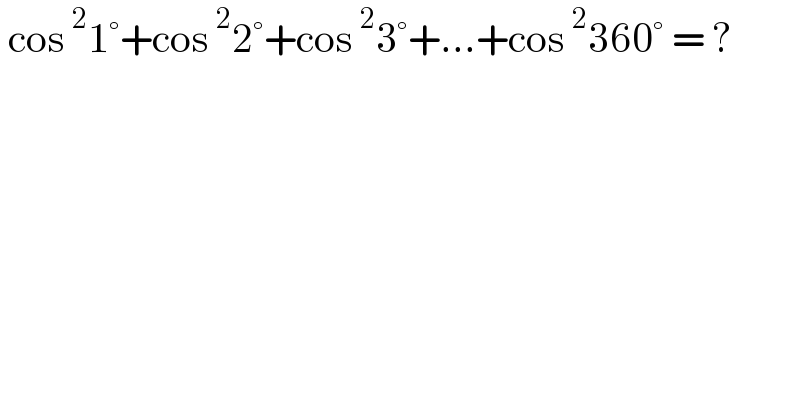
$$\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{1}°+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}°+\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}°+…+\mathrm{cos}\:^{\mathrm{2}} \mathrm{360}°\:=\:? \\ $$
Answered by Dwaipayan Shikari last updated on 01/Jul/21
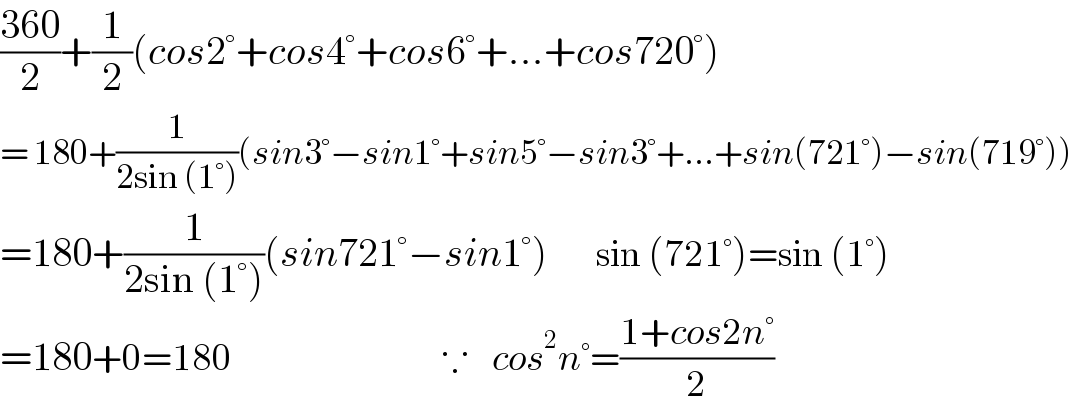
$$\frac{\mathrm{360}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}°+{cos}\mathrm{4}°+{cos}\mathrm{6}°+…+{cos}\mathrm{720}°\right) \\ $$$$=\:\mathrm{180}+\frac{\mathrm{1}}{\mathrm{2sin}\:\left(\mathrm{1}°\right)}\left({sin}\mathrm{3}°−{sin}\mathrm{1}°+{sin}\mathrm{5}°−{sin}\mathrm{3}°+…+{sin}\left(\mathrm{721}°\right)−{sin}\left(\mathrm{719}°\right)\right) \\ $$$$=\mathrm{180}+\frac{\mathrm{1}}{\mathrm{2sin}\:\left(\mathrm{1}°\right)}\left({sin}\mathrm{721}°−{sin}\mathrm{1}°\right)\:\:\:\:\:\:\:\:\mathrm{sin}\:\left(\mathrm{721}°\right)=\mathrm{sin}\:\left(\mathrm{1}°\right) \\ $$$$=\mathrm{180}+\mathrm{0}=\mathrm{180}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\:\:\:{cos}^{\mathrm{2}} {n}°=\frac{\mathrm{1}+{cos}\mathrm{2}{n}°}{\mathrm{2}} \\ $$
