Question Number 88507 by jagoll last updated on 11/Apr/20
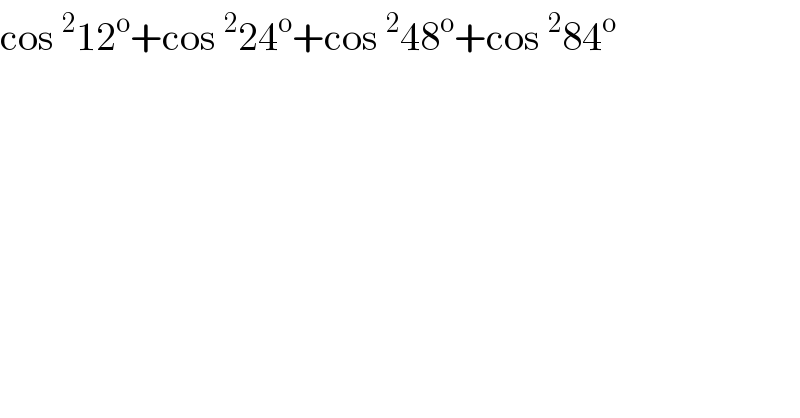
$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{12}^{\mathrm{o}} +\mathrm{cos}\:^{\mathrm{2}} \mathrm{24}^{\mathrm{o}} +\mathrm{cos}\:^{\mathrm{2}} \mathrm{48}^{\mathrm{o}} +\mathrm{cos}\:^{\mathrm{2}} \mathrm{84}^{\mathrm{o}} \\ $$
Commented by john santu last updated on 11/Apr/20
![cos^2 (84^o )=sin^2 (6^o ) ⇒[1−2sin^2 (6^o )]^2 + sin^2 (6^o ) + cos^2 (24^o ) + [2cos^2 (24^o )−1]^2 = 1−3sin^2 (6^o )+4sin^4 (6^o ) + 4cos^4 (24^o )−3cos^2 (24^o )+1 = 2−3(sin^2 (6^o )+cos^2 (24^o ))+ 4 (sin^4 (6^o )+cos^4 (24^o )) •)cos 24^o = cos (30^o −6^o ) cos 24^o = ((√3)/2) cos 6^o +(1/2)sin 6^o](https://www.tinkutara.com/question/Q88509.png)
$$\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{84}^{{o}} \right)=\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{6}^{{o}} \right) \\ $$$$\Rightarrow\left[\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{6}^{{o}} \right)\right]^{\mathrm{2}} +\:\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{6}^{{o}} \right)\:+\: \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{24}^{{o}} \right)\:+\:\left[\mathrm{2cos}\:^{\mathrm{2}} \left(\mathrm{24}^{{o}} \right)−\mathrm{1}\right]^{\mathrm{2}} \\ $$$$=\:\mathrm{1}−\mathrm{3sin}\:^{\mathrm{2}} \left(\mathrm{6}^{{o}} \right)+\mathrm{4sin}\:^{\mathrm{4}} \left(\mathrm{6}^{{o}} \right)\:+ \\ $$$$\mathrm{4cos}\:^{\mathrm{4}} \left(\mathrm{24}^{{o}} \right)−\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{24}^{{o}} \right)+\mathrm{1} \\ $$$$=\:\mathrm{2}−\mathrm{3}\left(\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{6}^{{o}} \right)+\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{24}^{{o}} \right)\right)+ \\ $$$$\mathrm{4}\:\left(\mathrm{sin}\:^{\mathrm{4}} \left(\mathrm{6}^{{o}} \right)+\mathrm{cos}\:^{\mathrm{4}} \left(\mathrm{24}^{{o}} \right)\right) \\ $$$$\left.\bullet\right)\mathrm{cos}\:\mathrm{24}^{{o}} \:=\:\mathrm{cos}\:\left(\mathrm{30}^{{o}} −\mathrm{6}^{{o}} \right) \\ $$$$\mathrm{cos}\:\mathrm{24}^{{o}} =\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{6}^{{o}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{6}^{{o}} \\ $$$$ \\ $$$$ \\ $$
Answered by som(math1967) last updated on 11/Apr/20

$$\left({cos}\mathrm{12}+{cos}\mathrm{48}\right)^{\mathrm{2}} −\mathrm{2}{cos}\mathrm{12}{cos}\mathrm{48} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({cos}\mathrm{24}+{cos}\mathrm{84}\right)^{\mathrm{2}} −\mathrm{2}{cos}\mathrm{24}{cos}\mathrm{84} \\ $$$$\left(\mathrm{2}{cos}\mathrm{30}{cos}\mathrm{18}\right)^{\mathrm{2}} +\left(\mathrm{2}{cos}\mathrm{30}{cos}\mathrm{54}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\left({cos}\mathrm{60}+{cos}\mathrm{36}\right)−\left({cos}\mathrm{60}+{cos}\mathrm{108}\right) \\ $$$$\mathrm{3}×\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\:+\mathrm{3}×\frac{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\:\:\:\:−\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}−{cos}\mathrm{72}\right) \\ $$$$=\frac{\mathrm{60}}{\mathrm{16}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{15}}{\mathrm{4}}\:−\mathrm{1}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}−\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{15}}{\mathrm{4}}\:−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{15}}{\mathrm{4}}\:−\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{4}}\:{ans} \\ $$$$ \\ $$
Commented by jagoll last updated on 11/Apr/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
