Question Number 169268 by amin96 last updated on 27/Apr/22
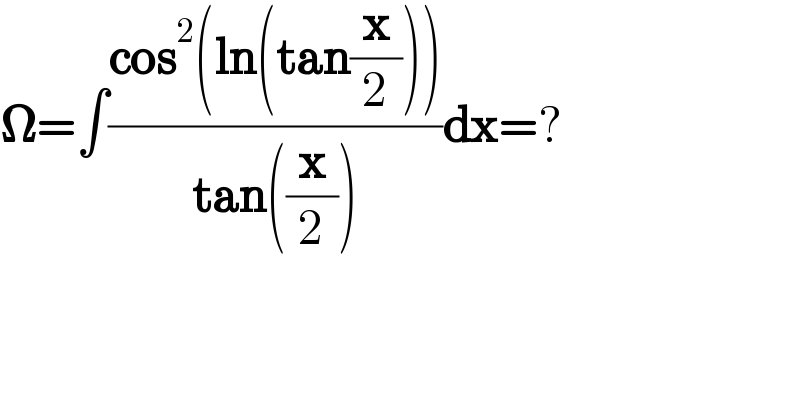
$$\boldsymbol{\Omega}=\int\frac{\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)\right)}{\boldsymbol{\mathrm{tan}}\left(\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)}\boldsymbol{\mathrm{dx}}=? \\ $$
Answered by Mathspace last updated on 28/Apr/22
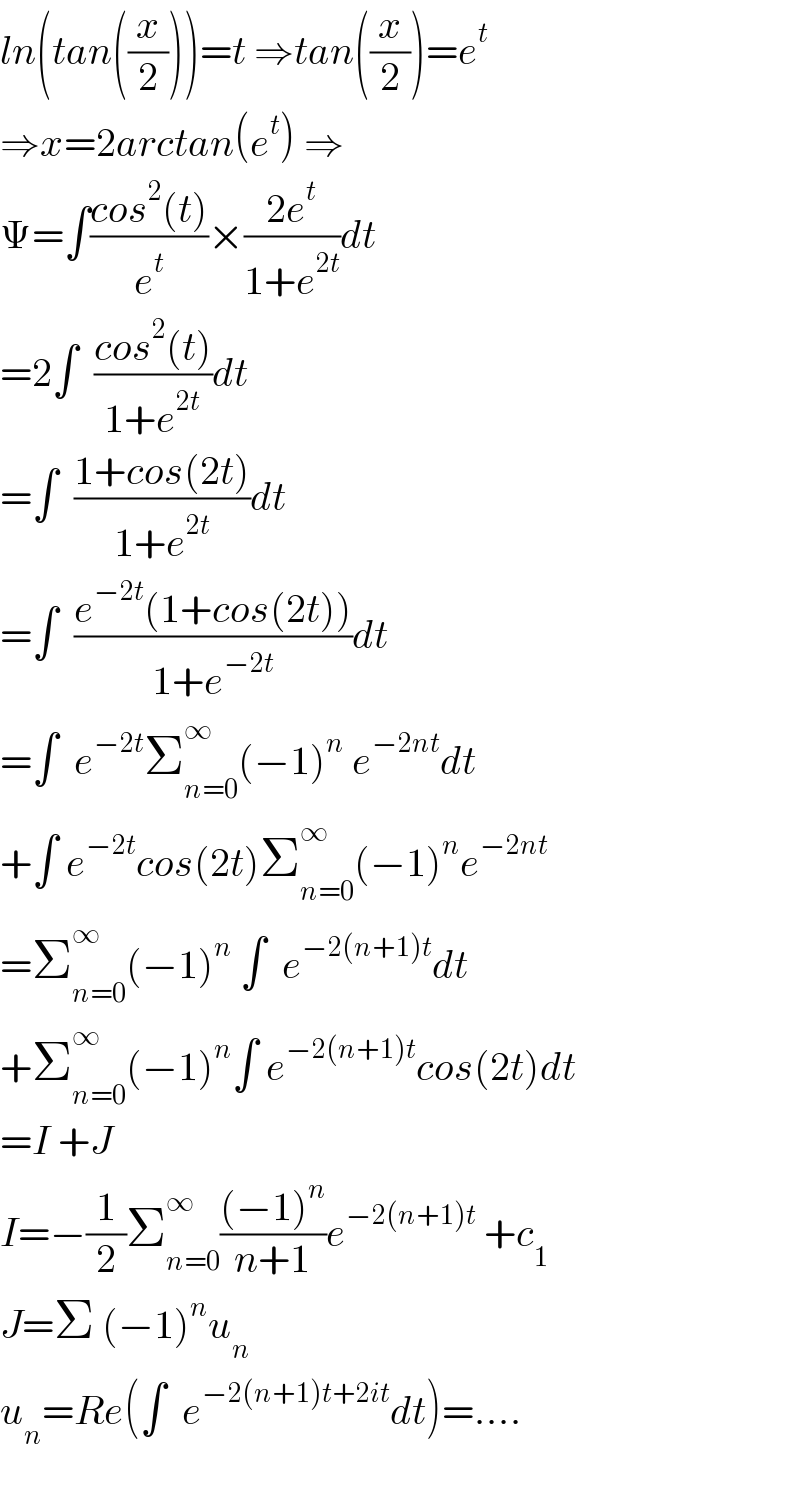
$${ln}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)={t}\:\Rightarrow{tan}\left(\frac{{x}}{\mathrm{2}}\right)={e}^{{t}} \\ $$$$\Rightarrow{x}=\mathrm{2}{arctan}\left({e}^{{t}} \right)\:\Rightarrow \\ $$$$\Psi=\int\frac{{cos}^{\mathrm{2}} \left({t}\right)}{{e}^{{t}} }×\frac{\mathrm{2}{e}^{{t}} }{\mathrm{1}+{e}^{\mathrm{2}{t}} }{dt} \\ $$$$=\mathrm{2}\int\:\:\frac{{cos}^{\mathrm{2}} \left({t}\right)}{\mathrm{1}+{e}^{\mathrm{2}{t}} }{dt} \\ $$$$=\int\:\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{e}^{\mathrm{2}{t}} }{dt} \\ $$$$=\int\:\:\frac{{e}^{−\mathrm{2}{t}} \left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right)}{\mathrm{1}+{e}^{−\mathrm{2}{t}} }{dt} \\ $$$$=\int\:\:{e}^{−\mathrm{2}{t}} \sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{2}{nt}} {dt} \\ $$$$+\int\:{e}^{−\mathrm{2}{t}} {cos}\left(\mathrm{2}{t}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {e}^{−\mathrm{2}{nt}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int\:\:{e}^{−\mathrm{2}\left({n}+\mathrm{1}\right){t}} {dt} \\ $$$$+\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \int\:{e}^{−\mathrm{2}\left({n}+\mathrm{1}\right){t}} {cos}\left(\mathrm{2}{t}\right){dt} \\ $$$$={I}\:+{J} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{e}^{−\mathrm{2}\left({n}+\mathrm{1}\right){t}} \:+{c}_{\mathrm{1}} \\ $$$${J}=\Sigma\:\left(−\mathrm{1}\right)^{{n}} {u}_{{n}} \\ $$$${u}_{{n}} ={Re}\left(\int\:\:{e}^{−\mathrm{2}\left({n}+\mathrm{1}\right){t}+\mathrm{2}{it}} {dt}\right)=…. \\ $$$$ \\ $$
