cos-2-x-sin-4-x-dx-

Question Number 79059 by jagoll last updated on 22/Jan/20

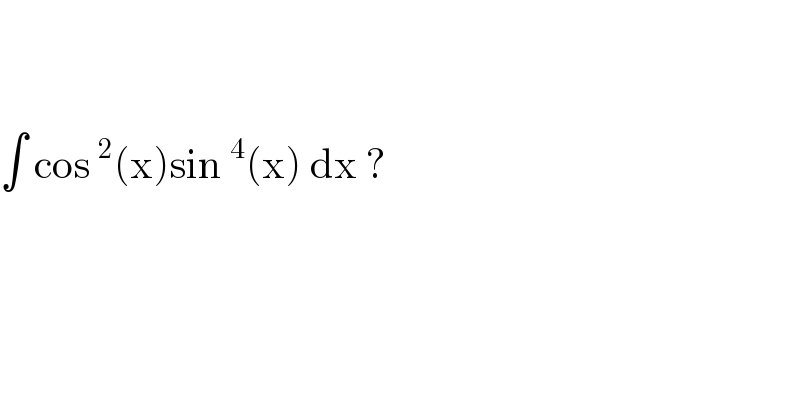
$$ \\ $$$$ \\ $$$$\int\:\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{sin}\:^{\mathrm{4}} \left(\mathrm{x}\right)\:\mathrm{dx}\:? \\ $$

Commented by john santu last updated on 22/Jan/20

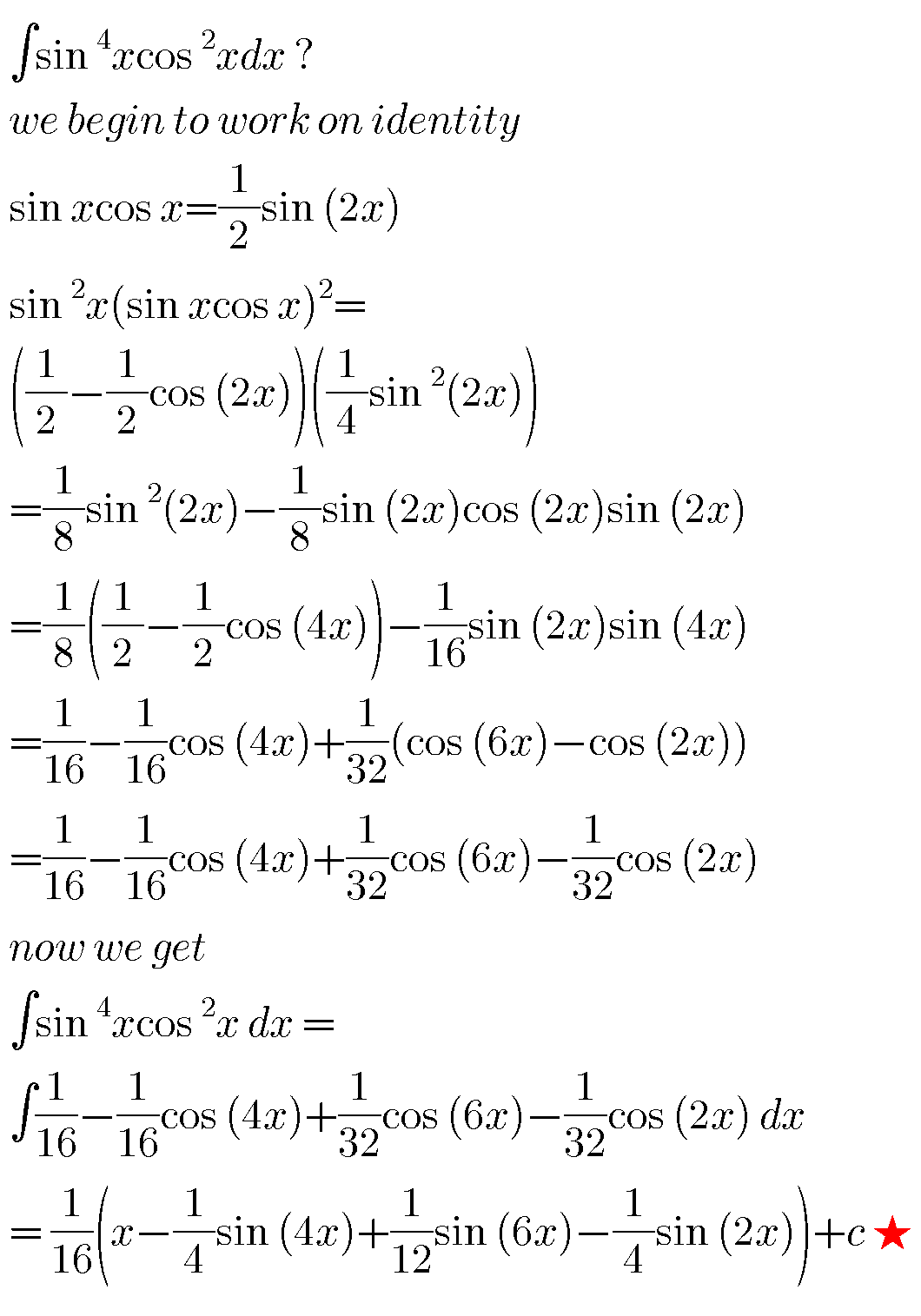
Commented by jagoll last updated on 22/Jan/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 22/Jan/20

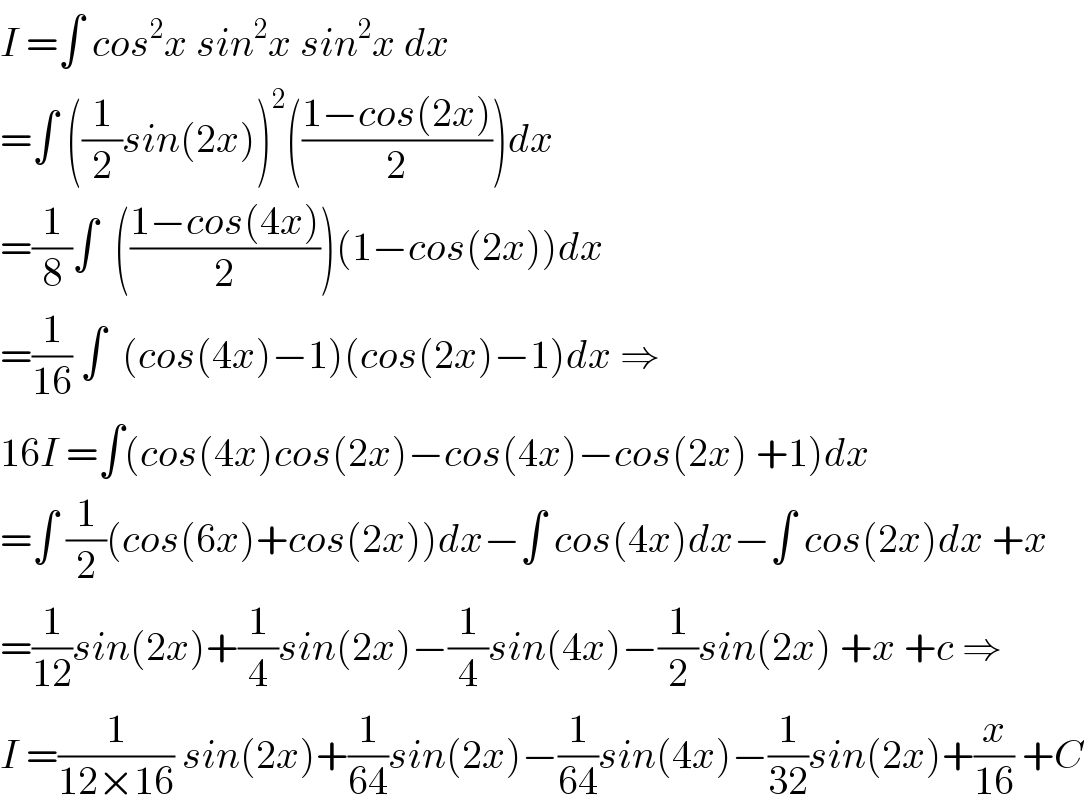
I =∫ cos^2 x sin^2 x sin^2 x dx =∫ ((1/2)sin(2x))^2 (((1−cos(2x))/2))dx =(1/8)∫ (((1−cos(4x))/2))(1−cos(2x))dx =(1/(16)) ∫ (cos(4x)−1)(cos(2x)−1)dx ⇒ 16I =∫(cos(4x)cos(2x)−cos(4x)−cos(2x) +1)dx =∫ (1/2)(cos(6x)+cos(2x))dx−∫ cos(4x)dx−∫ cos(2x)dx +x =(1/(12))sin(2x)+(1/4)sin(2x)−(1/4)sin(4x)−(1/2)sin(2x) +x +c ⇒ I =(1/(12×16)) sin(2x)+(1/(64))sin(2x)−(1/(64))sin(4x)−(1/(32))sin(2x)+(x/(16)) +C

$${I}\:=\int\:{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\:{dx} \\ $$$$=\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} \left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\left(\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\:\left({cos}\left(\mathrm{4}{x}\right)−\mathrm{1}\right)\left({cos}\left(\mathrm{2}{x}\right)−\mathrm{1}\right){dx}\:\Rightarrow \\ $$$$\mathrm{16}{I}\:=\int\left({cos}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{2}{x}\right)−{cos}\left(\mathrm{4}{x}\right)−{cos}\left(\mathrm{2}{x}\right)\:+\mathrm{1}\right){dx} \\ $$$$=\int\:\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\mathrm{6}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right){dx}−\int\:{cos}\left(\mathrm{4}{x}\right){dx}−\int\:{cos}\left(\mathrm{2}{x}\right){dx}\:+{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}{sin}\left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{4}{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\:+{x}\:+{c}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{12}×\mathrm{16}}\:{sin}\left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{64}}{sin}\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{64}}{sin}\left(\mathrm{4}{x}\right)−\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{2}{x}\right)+\frac{{x}}{\mathrm{16}}\:+{C} \\ $$

Commented by mathmax by abdo last updated on 22/Jan/20

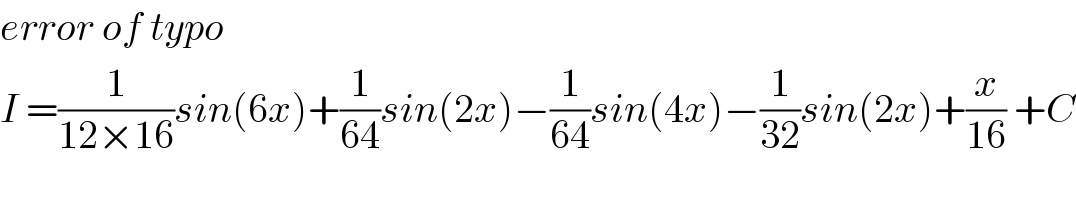
error of typo I =(1/(12×16))sin(6x)+(1/(64))sin(2x)−(1/(64))sin(4x)−(1/(32))sin(2x)+(x/(16)) +C

$${error}\:{of}\:{typo} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{12}×\mathrm{16}}{sin}\left(\mathrm{6}{x}\right)+\frac{\mathrm{1}}{\mathrm{64}}{sin}\left(\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{64}}{sin}\left(\mathrm{4}{x}\right)−\frac{\mathrm{1}}{\mathrm{32}}{sin}\left(\mathrm{2}{x}\right)+\frac{{x}}{\mathrm{16}}\:+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply