Question Number 144379 by imjagoll last updated on 25/Jun/21
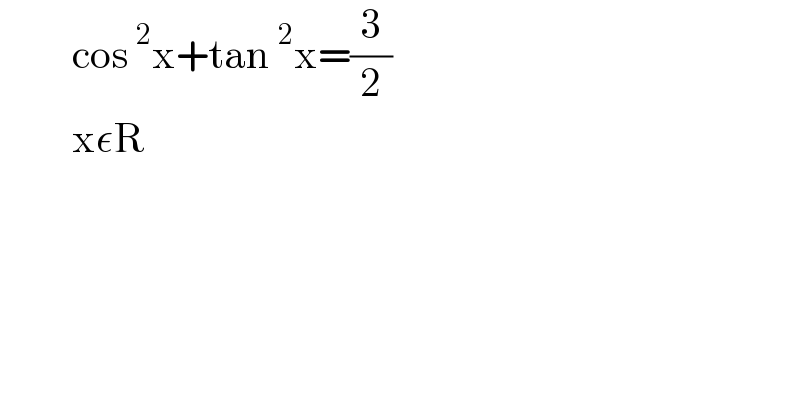
$$\:\:\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}\epsilon\mathrm{R}\: \\ $$
Answered by liberty last updated on 25/Jun/21
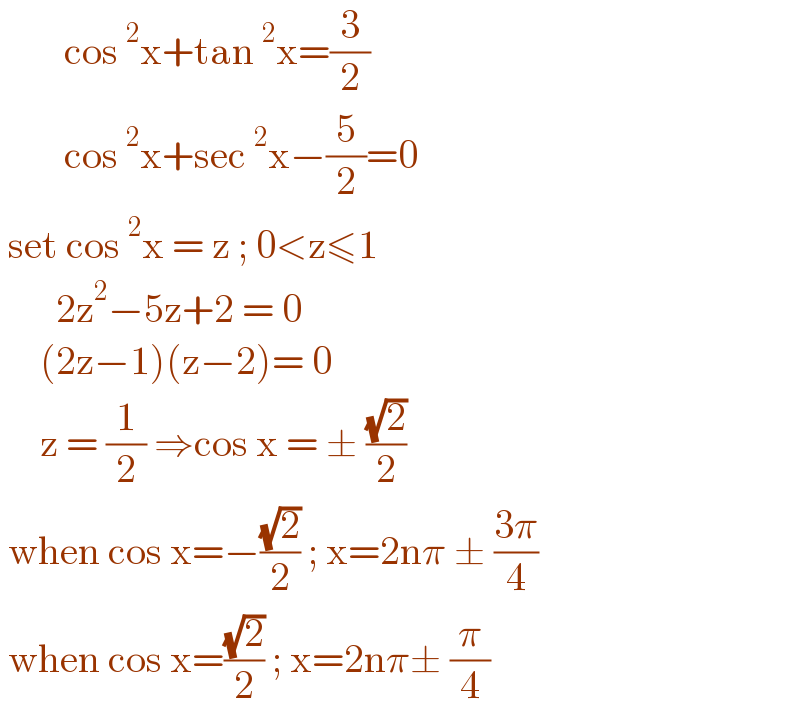
$$\:\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0} \\ $$$$\:\mathrm{set}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{z}\:;\:\mathrm{0}<\mathrm{z}\leqslant\mathrm{1}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{2z}^{\mathrm{2}} −\mathrm{5z}+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\left(\mathrm{2z}−\mathrm{1}\right)\left(\mathrm{z}−\mathrm{2}\right)=\:\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{z}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{cos}\:\mathrm{x}\:=\:\pm\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\:\mathrm{when}\:\mathrm{cos}\:\mathrm{x}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:;\:\mathrm{x}=\mathrm{2n}\pi\:\pm\:\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\:\mathrm{when}\:\mathrm{cos}\:\mathrm{x}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:;\:\mathrm{x}=\mathrm{2n}\pi\pm\:\frac{\pi}{\mathrm{4}} \\ $$
Answered by yoba last updated on 25/Jun/21
![cos^2 x+tan^2 x=cos^2 x+1+tan^2 x−1=cos^2 x+(1/(cos^2 x))−1=(3/2) •contraintes sur x: cosx≠0 ⇒ x∈ R\{−(π/2)[kπ], k∈Z} ⇒cos^2 x+(1/(cos^2 x))−(5/2)=0 ⇒cos^4 x−(5/2)cos^2 x+1=0 ⇒2cos^4 x−5cos^2 x+2=0 posons a=cos^2 x ⇒2a^2 −5a+2=0 ⇒△=25−4×4=9=3^2 ⇒a=(1/2) ou a=2 ⇒ cos^2 x=(1/2) ou cos^2 x=2(impossible) ⇒ cosx=((√2)/2) ou cosx=−((√2)/2)](https://www.tinkutara.com/question/Q144407.png)
$$\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\mathrm{1}+\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}−\mathrm{1}=\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}−\mathrm{1}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\bullet\boldsymbol{\mathrm{contraintes}}\:\boldsymbol{\mathrm{sur}}\:\boldsymbol{\mathrm{x}}:\:\boldsymbol{\mathrm{cosx}}\neq\mathrm{0}\:\Rightarrow\:\boldsymbol{\mathrm{x}}\in\:\mathbb{R}\backslash\left\{−\frac{\pi}{\mathrm{2}}\left[\boldsymbol{\mathrm{k}}\pi\right],\:\boldsymbol{\mathrm{k}}\in\mathbb{Z}\right\} \\ $$$$\Rightarrow\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}−\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\boldsymbol{\mathrm{cos}}^{\mathrm{4}} \boldsymbol{\mathrm{x}}−\frac{\mathrm{5}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{4}} \boldsymbol{\mathrm{x}}−\mathrm{5}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\mathrm{2}=\mathrm{0}\:\boldsymbol{\mathrm{posons}}\:\boldsymbol{\mathrm{a}}=\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{a}}+\mathrm{2}=\mathrm{0}\:\Rightarrow\bigtriangleup=\mathrm{25}−\mathrm{4}×\mathrm{4}=\mathrm{9}=\mathrm{3}^{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{a}}=\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{\mathrm{ou}}\:\boldsymbol{\mathrm{a}}=\mathrm{2} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{\mathrm{ou}}\:\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}=\mathrm{2}\left(\boldsymbol{\mathrm{impossible}}\right) \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{cosx}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\boldsymbol{\mathrm{ou}}\:\boldsymbol{\mathrm{cosx}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
