Question Number 121224 by liberty last updated on 06/Nov/20

$$\:\:\:\:\int\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{tan}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{dx}\: \\ $$
Answered by benjo_mathlover last updated on 06/Nov/20
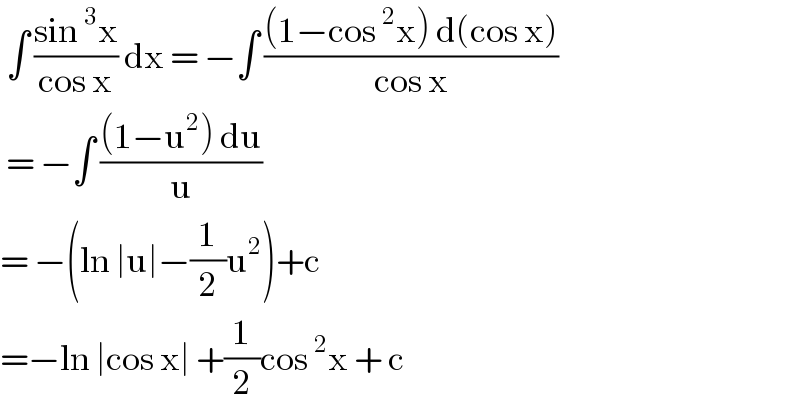
$$\:\int\:\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=\:−\int\:\frac{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)\:\mathrm{d}\left(\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:=\:−\int\:\frac{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\:\mathrm{du}}{\mathrm{u}} \\ $$$$=\:−\left(\mathrm{ln}\:\mid\mathrm{u}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}^{\mathrm{2}} \right)+\mathrm{c}\: \\ $$$$=−\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{x}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:+\:\mathrm{c} \\ $$
