Question Number 118575 by bramlexs22 last updated on 18/Oct/20
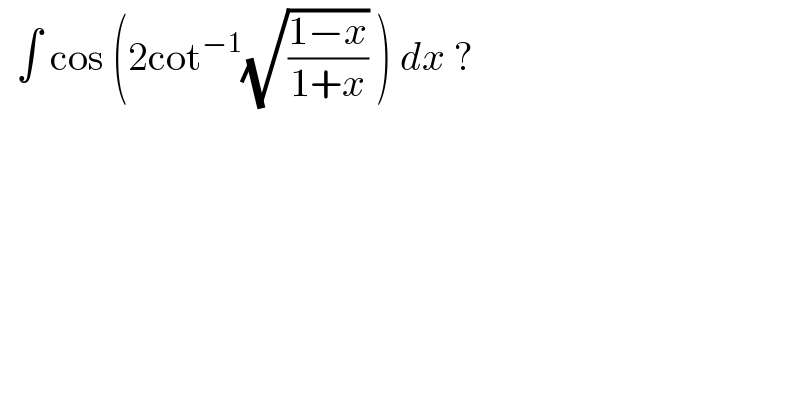
$$\:\:\int\:\mathrm{cos}\:\left(\mathrm{2cot}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:\right)\:{dx}\:? \\ $$
Answered by benjo_mathlover last updated on 18/Oct/20
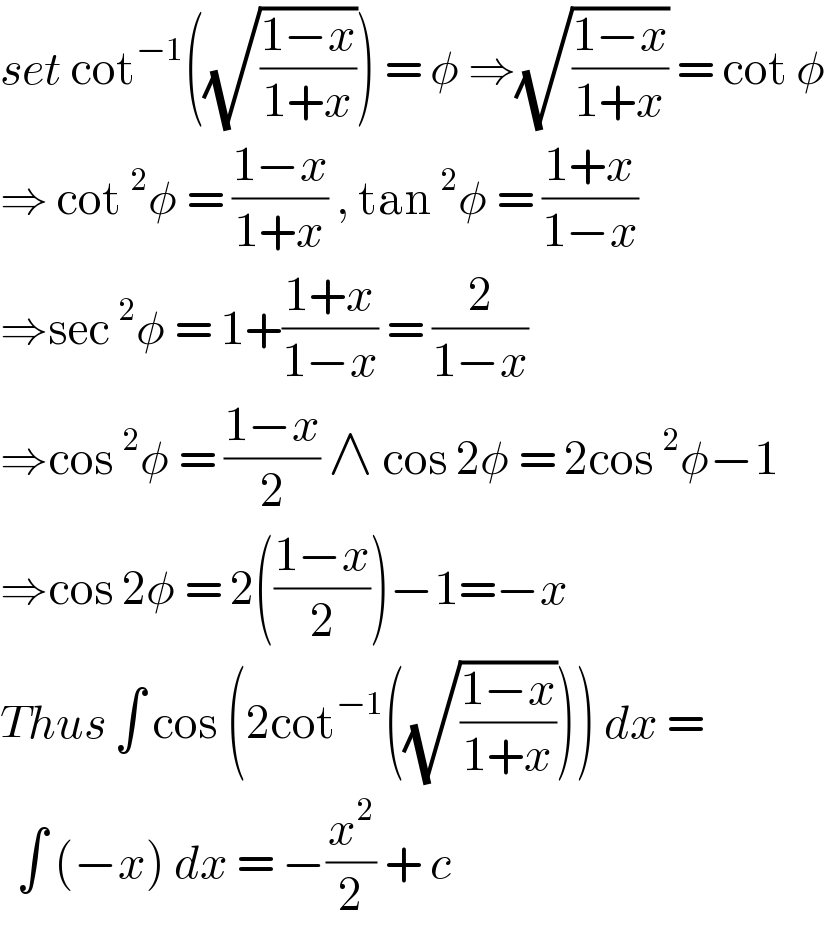
$${set}\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\right)\:=\:\phi\:\Rightarrow\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:=\:\mathrm{cot}\:\phi \\ $$$$\Rightarrow\:\mathrm{cot}\:^{\mathrm{2}} \phi\:=\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:,\:\mathrm{tan}\:^{\mathrm{2}} \phi\:=\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow\mathrm{sec}\:^{\mathrm{2}} \phi\:=\:\mathrm{1}+\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\:=\:\frac{\mathrm{2}}{\mathrm{1}−{x}}\: \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} \phi\:=\:\frac{\mathrm{1}−{x}}{\mathrm{2}}\:\wedge\:\mathrm{cos}\:\mathrm{2}\phi\:=\:\mathrm{2cos}\:^{\mathrm{2}} \phi−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\phi\:=\:\mathrm{2}\left(\frac{\mathrm{1}−{x}}{\mathrm{2}}\right)−\mathrm{1}=−{x} \\ $$$${Thus}\:\int\:\mathrm{cos}\:\left(\mathrm{2cot}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\right)\right)\:{dx}\:= \\ $$$$\:\:\int\:\left(−{x}\right)\:{dx}\:=\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\:{c}\: \\ $$
