Question Number 50466 by afachri last updated on 16/Dec/18
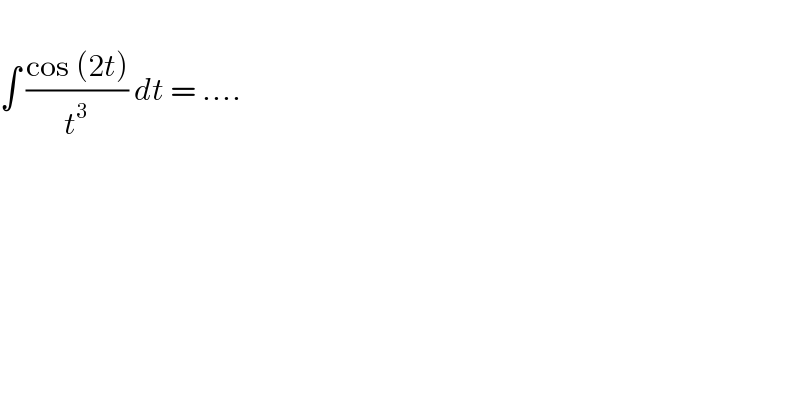
$$\: \\ $$$$\int\:\frac{\mathrm{cos}\:\left(\mathrm{2}{t}\right)}{{t}^{\mathrm{3}} }\:{dt}\:=\:…. \\ $$
Commented by afachri last updated on 16/Dec/18
$$\boldsymbol{\mathrm{Would}}\:\boldsymbol{\mathrm{anybody}}\:\boldsymbol{\mathrm{give}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{hand}} \\ $$$$\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{this}}\:?\:\boldsymbol{\mathrm{i}}'\boldsymbol{\mathrm{m}}\:\boldsymbol{\mathrm{stuck}}.\: \\ $$
Commented by maxmathsup by imad last updated on 16/Dec/18
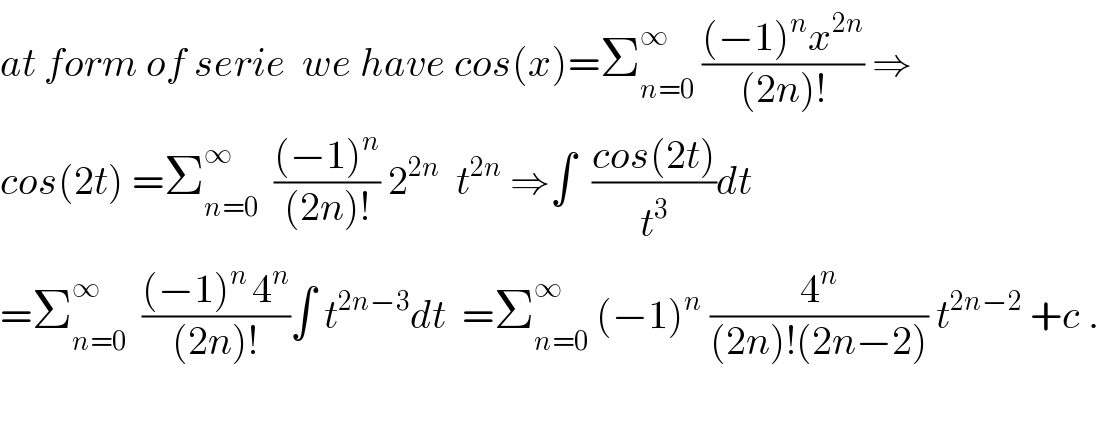
$${at}\:{form}\:{of}\:{serie}\:\:{we}\:{have}\:{cos}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:\Rightarrow \\ $$$${cos}\left(\mathrm{2}{t}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\:\mathrm{2}^{\mathrm{2}{n}} \:\:{t}^{\mathrm{2}{n}} \:\Rightarrow\int\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{{t}^{\mathrm{3}} }{dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}\:} \mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!}\int\:{t}^{\mathrm{2}{n}−\mathrm{3}} {dt}\:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\frac{\mathrm{4}^{{n}} }{\left(\mathrm{2}{n}\right)!\left(\mathrm{2}{n}−\mathrm{2}\right)}\:{t}^{\mathrm{2}{n}−\mathrm{2}} \:+{c}\:. \\ $$$$ \\ $$
Commented by afachri last updated on 17/Dec/18
$$\mathrm{aha},\:\mathrm{it}'\mathrm{s}\:\mathrm{McLaurin}\:\mathrm{series}\:\mathrm{Sir}.\:\mathrm{Thank}\:\mathrm{u} \\ $$$$\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$
Commented by maxmathsup by imad last updated on 17/Dec/18
$${you}\:{are}\:{welcome}. \\ $$
