Question Number 85349 by john santu last updated on 21/Mar/20
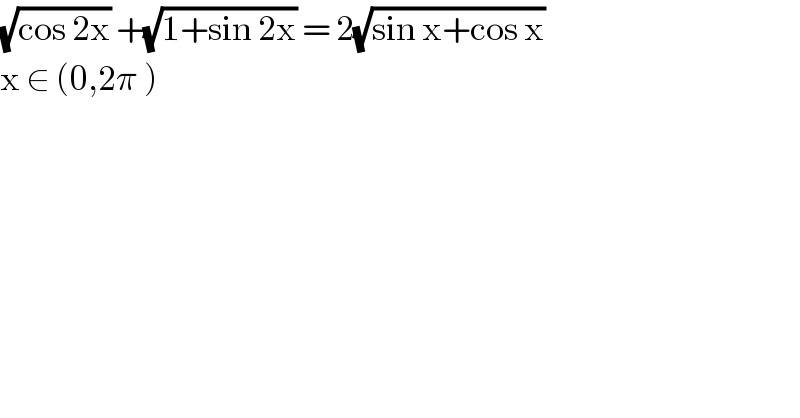
$$\sqrt{\mathrm{cos}\:\mathrm{2x}}\:+\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}\:=\:\mathrm{2}\sqrt{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\: \\ $$$$\mathrm{x}\:\in\:\left(\mathrm{0},\mathrm{2}\pi\:\right) \\ $$
Commented by john santu last updated on 21/Mar/20
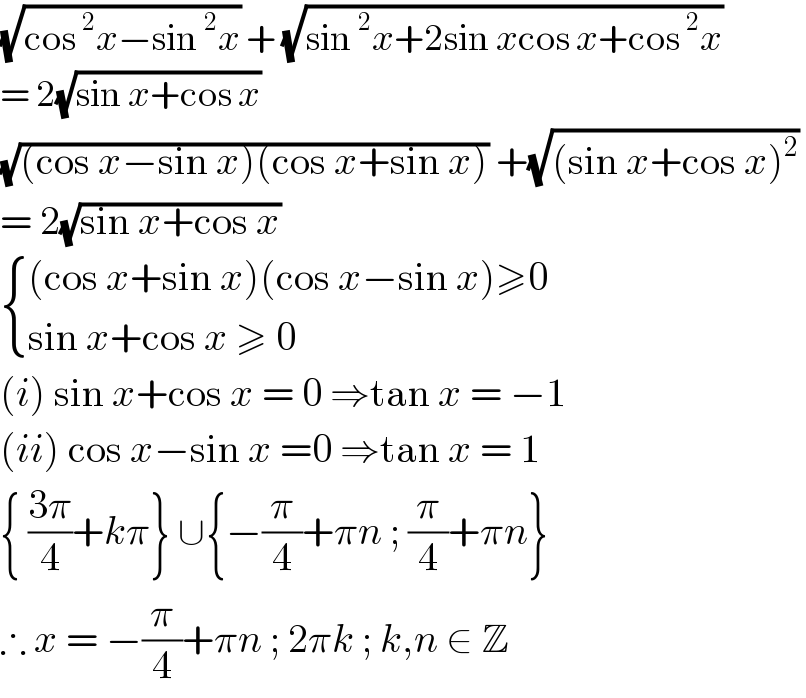
$$\sqrt{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:+\:\sqrt{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}+\mathrm{cos}\:^{\mathrm{2}} {x}}\: \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\: \\ $$$$\sqrt{\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)}\:+\sqrt{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\: \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\: \\ $$$$\begin{cases}{\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\geqslant\mathrm{0}}\\{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:\geqslant\:\mathrm{0}}\end{cases} \\ $$$$\left({i}\right)\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:\mathrm{0}\:\Rightarrow\mathrm{tan}\:{x}\:=\:−\mathrm{1} \\ $$$$\left({ii}\right)\:\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\:=\mathrm{0}\:\Rightarrow\mathrm{tan}\:{x}\:=\:\mathrm{1} \\ $$$$\left\{\:\frac{\mathrm{3}\pi}{\mathrm{4}}+{k}\pi\right\}\:\cup\left\{−\frac{\pi}{\mathrm{4}}+\pi{n}\:;\:\frac{\pi}{\mathrm{4}}+\pi{n}\right\} \\ $$$$\therefore\:{x}\:=\:−\frac{\pi}{\mathrm{4}}+\pi{n}\:;\:\mathrm{2}\pi{k}\:;\:{k},{n}\:\in\:\mathbb{Z} \\ $$
