Question Number 43267 by Rauny last updated on 09/Sep/18
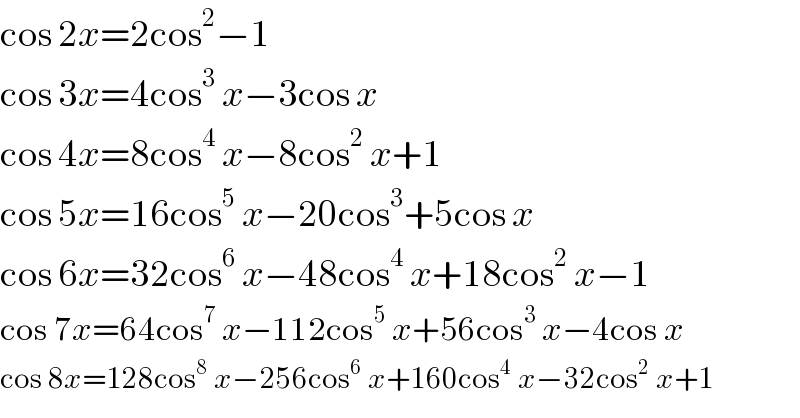
$$\mathrm{cos}\:\mathrm{2}{x}=\mathrm{2cos}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{3}{x}=\mathrm{4cos}^{\mathrm{3}} \:{x}−\mathrm{3cos}\:{x} \\ $$$$\mathrm{cos}\:\mathrm{4}{x}=\mathrm{8cos}^{\mathrm{4}} \:{x}−\mathrm{8cos}^{\mathrm{2}} \:{x}+\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{5}{x}=\mathrm{16cos}^{\mathrm{5}} \:{x}−\mathrm{20cos}^{\mathrm{3}} +\mathrm{5cos}\:{x}\: \\ $$$$\mathrm{cos}\:\mathrm{6}{x}=\mathrm{32cos}^{\mathrm{6}} \:{x}−\mathrm{48cos}^{\mathrm{4}} \:{x}+\mathrm{18cos}^{\mathrm{2}} \:{x}−\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{7}{x}=\mathrm{64cos}^{\mathrm{7}} \:{x}−\mathrm{112cos}^{\mathrm{5}} \:{x}+\mathrm{56cos}^{\mathrm{3}} \:{x}−\mathrm{4cos}\:{x} \\ $$$$\mathrm{cos}\:\mathrm{8}{x}=\mathrm{128cos}^{\mathrm{8}} \:{x}−\mathrm{256cos}^{\mathrm{6}} \:{x}+\mathrm{160cos}^{\mathrm{4}} \:{x}−\mathrm{32cos}^{\mathrm{2}} \:{x}+\mathrm{1} \\ $$
Commented by malwaan last updated on 09/Sep/18

$$? \\ $$
Commented by Rauny last updated on 09/Sep/18

$$\because\mathrm{cos}\:\left({a}+{b}\right)=\mathrm{cos}\:{a}\mathrm{cos}\:{b}−\mathrm{sin}\:{a}\mathrm{sin}\:{b} \\ $$$$\mathrm{sin}\:\left({a}+{b}\right)=\mathrm{sin}\:{a}\mathrm{cos}\:{b}+\mathrm{cos}\:{a}\mathrm{sin}\:{b} \\ $$
