Question Number 89123 by john santu last updated on 15/Apr/20
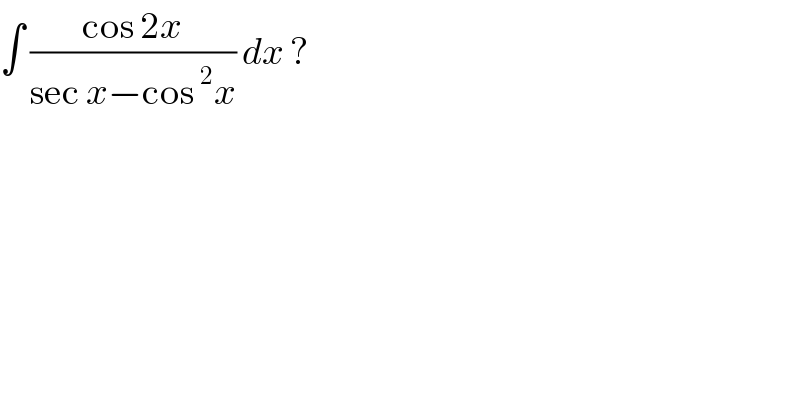
$$\int\:\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{sec}\:{x}−\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:? \\ $$
Commented by MJS last updated on 15/Apr/20
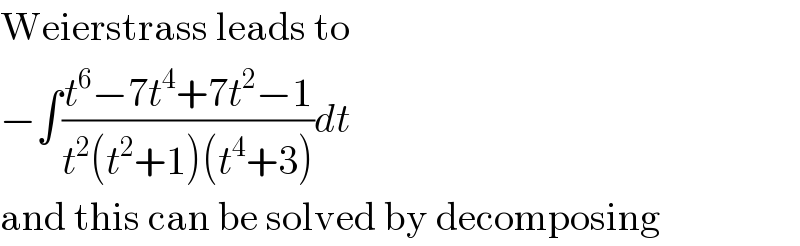
$$\mathrm{Weierstrass}\:\mathrm{leads}\:\mathrm{to} \\ $$$$−\int\frac{{t}^{\mathrm{6}} −\mathrm{7}{t}^{\mathrm{4}} +\mathrm{7}{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{3}\right)}{dt} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{decomposing} \\ $$
Commented by john santu last updated on 15/Apr/20
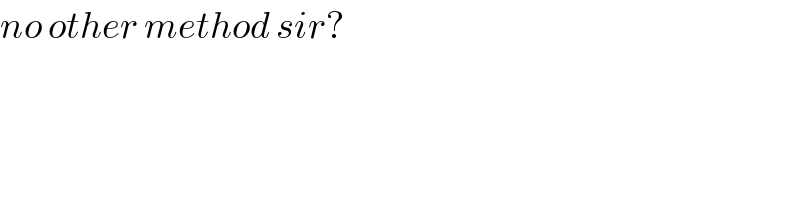
$${no}\:{other}\:{method}\:{sir}? \\ $$
Commented by MJS last updated on 15/Apr/20
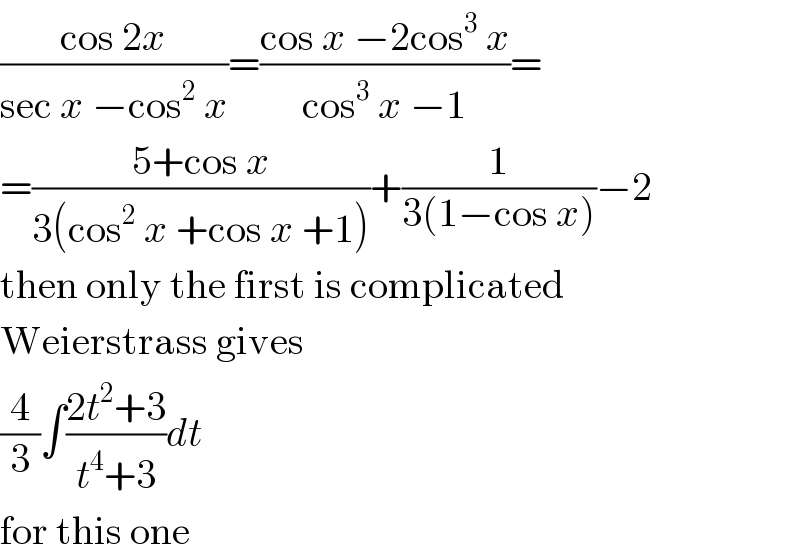
$$\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{sec}\:{x}\:−\mathrm{cos}^{\mathrm{2}} \:{x}}=\frac{\mathrm{cos}\:{x}\:−\mathrm{2cos}^{\mathrm{3}} \:{x}}{\mathrm{cos}^{\mathrm{3}} \:{x}\:−\mathrm{1}}= \\ $$$$=\frac{\mathrm{5}+\mathrm{cos}\:{x}}{\mathrm{3}\left(\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{cos}\:{x}\:+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}−\mathrm{2} \\ $$$$\mathrm{then}\:\mathrm{only}\:\mathrm{the}\:\mathrm{first}\:\mathrm{is}\:\mathrm{complicated} \\ $$$$\mathrm{Weierstrass}\:\mathrm{gives} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\int\frac{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}}{{t}^{\mathrm{4}} +\mathrm{3}}{dt} \\ $$$$\mathrm{for}\:\mathrm{this}\:\mathrm{one} \\ $$
Commented by john santu last updated on 15/Apr/20
$${oo}\:{yes}.\:{thank}\:{you}\:{sir} \\ $$
