Question Number 20465 by tammi last updated on 27/Aug/17
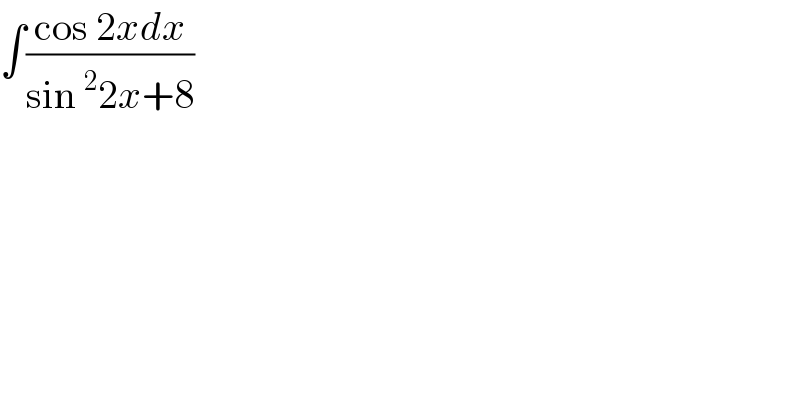
$$\int\frac{\mathrm{cos}\:\mathrm{2}{xdx}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{8}} \\ $$
Answered by sma3l2996 last updated on 27/Aug/17
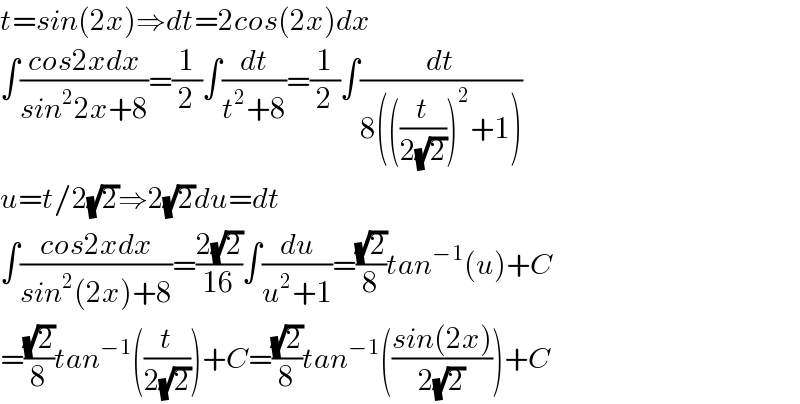
$${t}={sin}\left(\mathrm{2}{x}\right)\Rightarrow{dt}=\mathrm{2}{cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$\int\frac{{cos}\mathrm{2}{xdx}}{{sin}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{8}\left(\left(\frac{{t}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${u}={t}/\mathrm{2}\sqrt{\mathrm{2}}\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{du}={dt} \\ $$$$\int\frac{{cos}\mathrm{2}{xdx}}{{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)+\mathrm{8}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{16}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}{tan}^{−\mathrm{1}} \left({u}\right)+{C} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}{tan}^{−\mathrm{1}} \left(\frac{{t}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+{C}=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}{tan}^{−\mathrm{1}} \left(\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+{C} \\ $$
