Question Number 80739 by jagoll last updated on 05/Feb/20

$$\mathrm{cos}\:^{\mathrm{3}} \theta+\mathrm{2sin}\:^{\mathrm{2}} \theta=\mathrm{3}\bar {\:}\theta\in\left(\mathrm{0},\mathrm{2}\pi\right) \\ $$$${what}\:{is}\:\theta\:? \\ $$
Commented by mr W last updated on 06/Feb/20
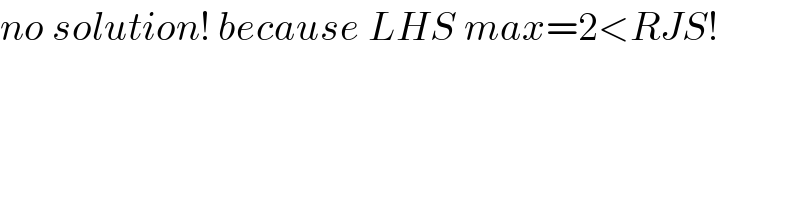
$${no}\:{solution}!\:{because}\:{LHS}\:{max}=\mathrm{2}<{RJS}! \\ $$
Commented by hknkrc46 last updated on 06/Feb/20

$${sin}^{\mathrm{2}} \theta=\mathrm{1}−{cos}^{\mathrm{2}} \theta \\ $$$${cos}^{\mathrm{3}} \theta+\mathrm{2}\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)=\mathrm{3} \\ $$$${cos}^{\mathrm{3}} \theta+\mathrm{2}−\mathrm{2}{cos}^{\mathrm{2}} \theta=\mathrm{3} \\ $$$${cos}^{\mathrm{3}} \theta−\mathrm{2}{cos}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$${cos}^{\mathrm{2}} \theta\left({cos}\theta−\mathrm{2}\right)=\mathrm{1} \\ $$$$−\mathrm{1}\leqslant{cos}\theta\leqslant\mathrm{1}\Rightarrow−\mathrm{3}\leqslant{cos}\theta−\mathrm{2}\leqslant−\mathrm{1} \\ $$$$\Rightarrow{cos}^{\mathrm{2}} \theta<\mathrm{0}\Rightarrow\theta\notin\left(\mathrm{0},\mathrm{2}\pi\right) \\ $$
