Menu Close

cos-4-x-sin-4-x-cos2x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 64802 by mmkkmm000m last updated on 21/Jul/19
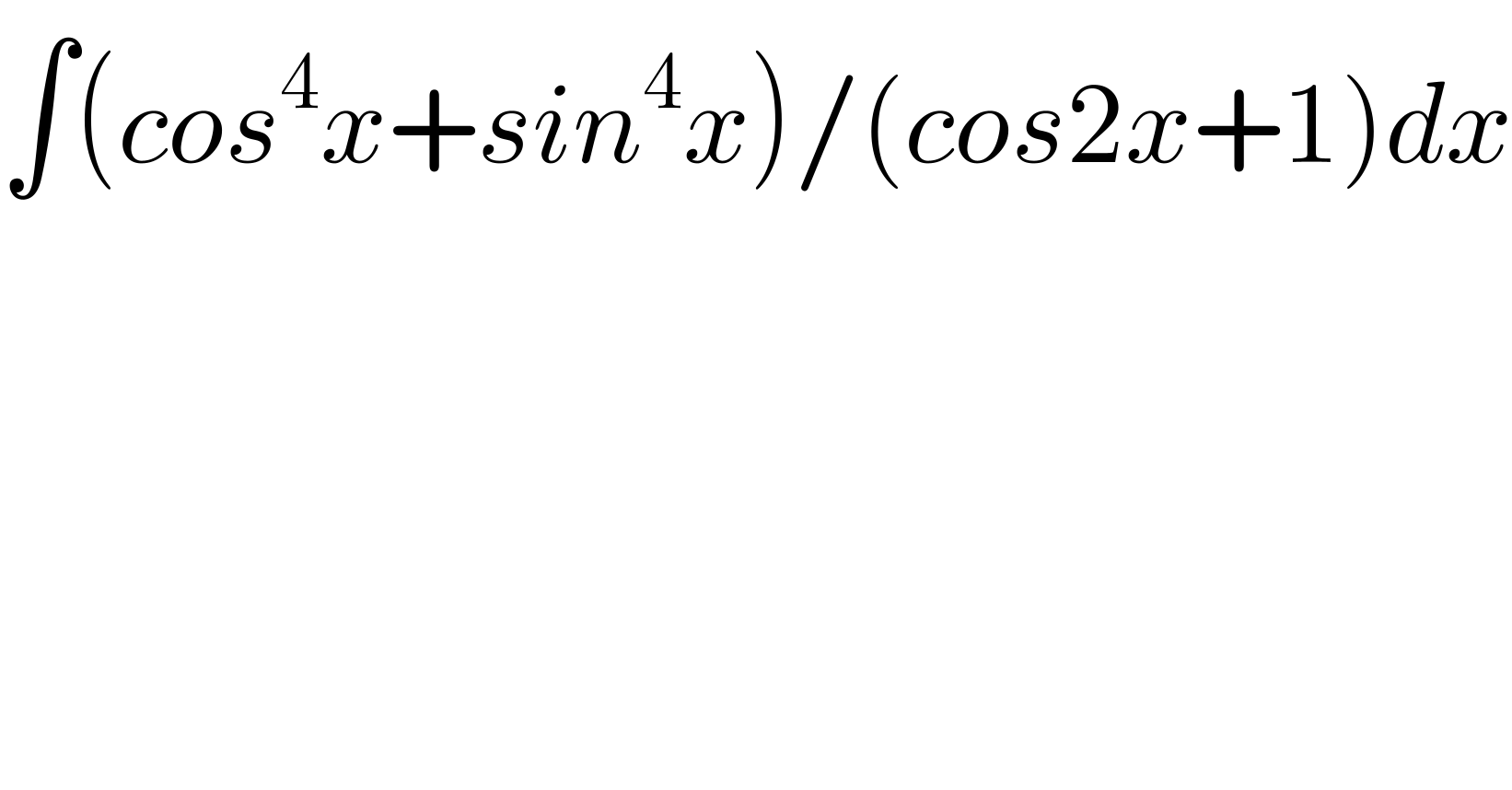
∫(cos^4 x+sin^4 x)/(cos2x+1)dx
$$\int\left({cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}\right)/\left({cos}\mathrm{2}{x}+\mathrm{1}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19
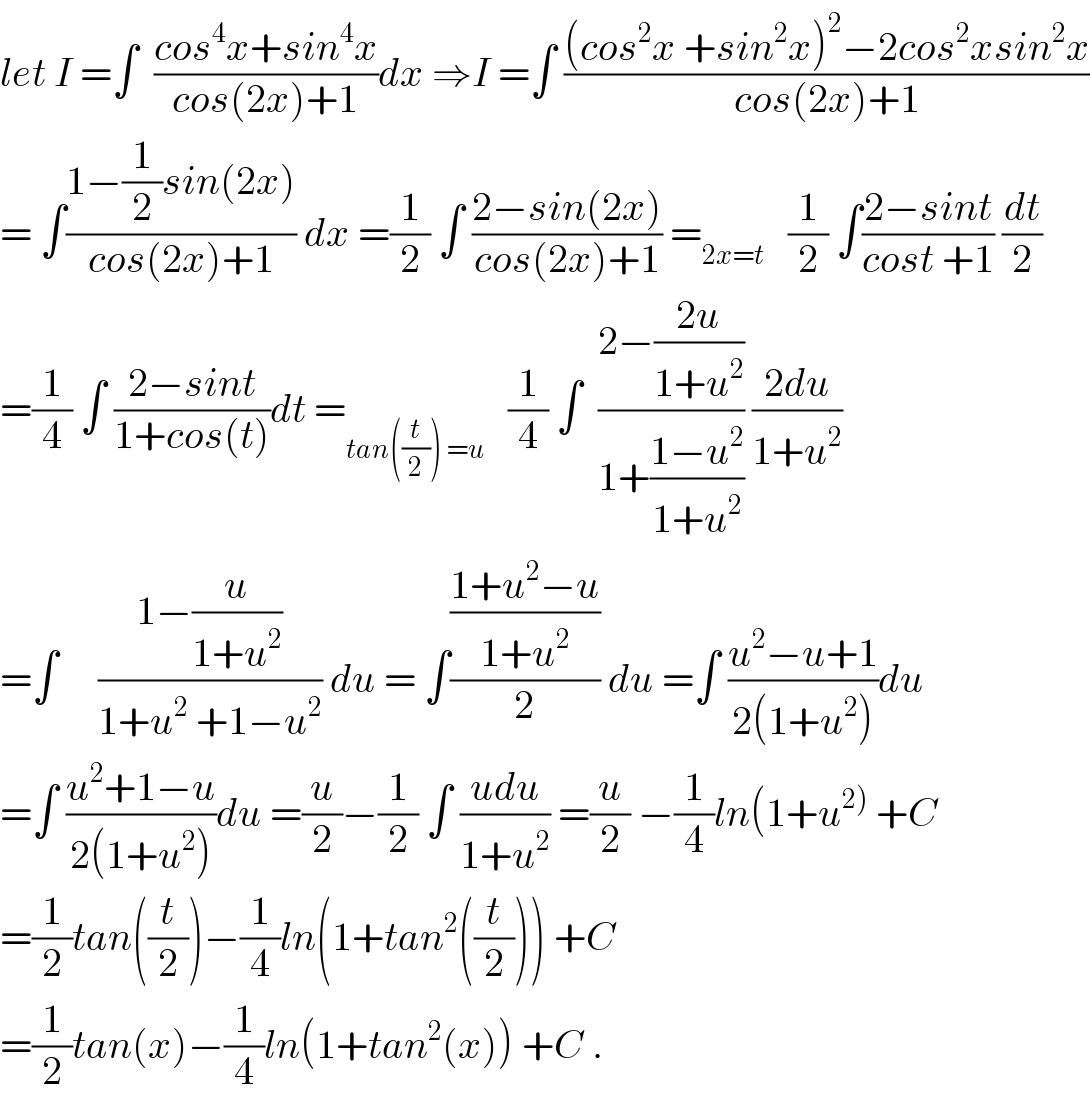
let I =∫ ((cos^4 x+sin^4 x)/(cos(2x)+1))dx ⇒I =∫ (((cos^2 x +sin^2 x)^2 −2cos^2 xsin^2 x)/(cos(2x)+1)) = ∫((1−(1/2)sin(2x))/(cos(2x)+1)) dx =(1/2) ∫ ((2−sin(2x))/(cos(2x)+1)) =_(2x=t) (1/2) ∫((2−sint)/(cost +1)) (dt/2) =(1/4) ∫ ((2−sint)/(1+cos(t)))dt =_(tan((t/2)) =u) (1/4) ∫ ((2−((2u)/(1+u^2 )))/(1+((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) =∫ ((1−(u/(1+u^2 )))/(1+u^2 +1−u^2 )) du = ∫(((1+u^2 −u)/(1+u^2 ))/2) du =∫ ((u^2 −u+1)/(2(1+u^2 )))du =∫ ((u^2 +1−u)/(2(1+u^2 )))du =(u/2)−(1/2) ∫ ((udu)/(1+u^2 )) =(u/2) −(1/4)ln(1+u^(2)) +C =(1/2)tan((t/2))−(1/4)ln(1+tan^2 ((t/2))) +C =(1/2)tan(x)−(1/4)ln(1+tan^2 (x)) +C .
$${let}\:{I}\:=\int\:\:\frac{{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}}{{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}}{dx}\:\Rightarrow{I}\:=\int\:\frac{\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}}{{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}} \\ $$$$=\:\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)}{{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}−{sin}\left(\mathrm{2}{x}\right)}{{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}}\:=_{\mathrm{2}{x}={t}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\frac{\mathrm{2}−{sint}}{{cost}\:+\mathrm{1}}\:\frac{{dt}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\frac{\mathrm{2}−{sint}}{\mathrm{1}+{cos}\left({t}\right)}{dt}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={u}} \:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\frac{\mathrm{2}−\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\:\:\frac{\mathrm{1}−\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }\:{du}\:=\:\int\frac{\frac{\mathrm{1}+{u}^{\mathrm{2}} −{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{2}}\:{du}\:=\int\:\frac{{u}^{\mathrm{2}} −{u}+\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$=\int\:\frac{{u}^{\mathrm{2}} +\mathrm{1}−{u}}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du}\:=\frac{{u}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{{udu}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{{u}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{u}^{\left.\mathrm{2}\right)} \:+{C}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{tan}\left(\frac{{t}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{tan}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)\right)\:+{C}\:. \\ $$
Answered by Tanmay chaudhury last updated on 21/Jul/19
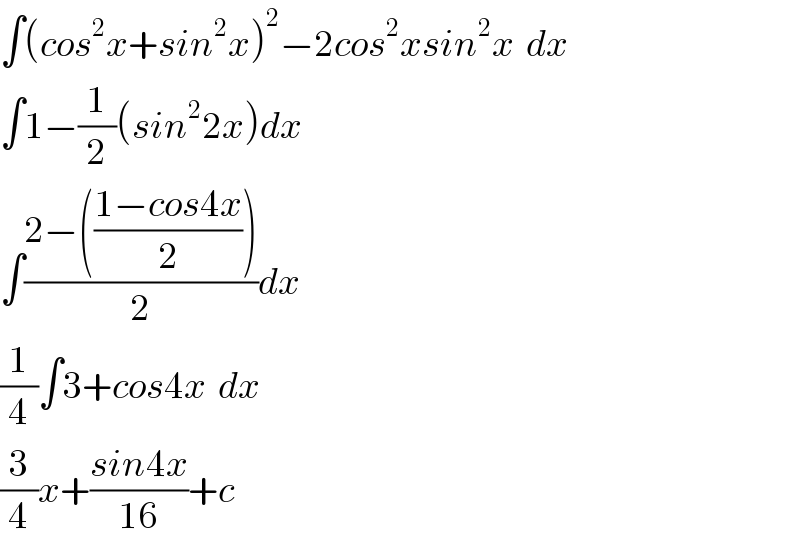
∫(cos^2 x+sin^2 x)^2 −2cos^2 xsin^2 x dx ∫1−(1/2)(sin^2 2x)dx ∫((2−(((1−cos4x)/2)))/2)dx (1/4)∫3+cos4x dx (3/4)x+((sin4x)/(16))+c
$$\int\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\:\:{dx} \\ $$$$\int\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left({sin}^{\mathrm{2}} \mathrm{2}{x}\right){dx} \\ $$$$\int\frac{\mathrm{2}−\left(\frac{\mathrm{1}−{cos}\mathrm{4}{x}}{\mathrm{2}}\right)}{\mathrm{2}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{3}+{cos}\mathrm{4}{x}\:\:{dx} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}{x}+\frac{{sin}\mathrm{4}{x}}{\mathrm{16}}+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *