Question Number 82954 by john santu last updated on 26/Feb/20
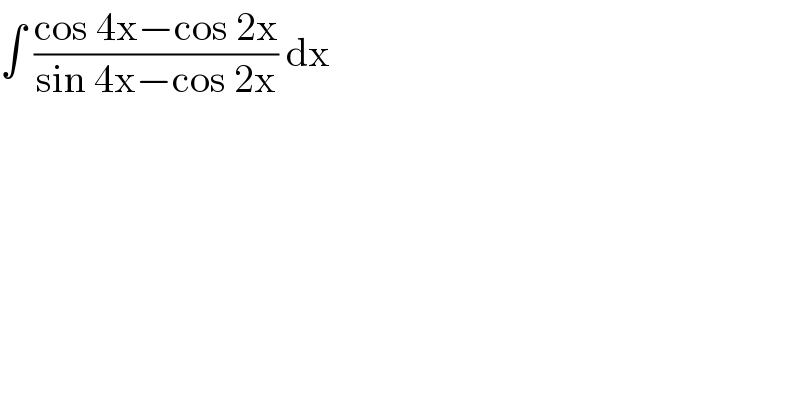
$$\int\:\frac{\mathrm{cos}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{sin}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{2x}}\:\mathrm{dx}\: \\ $$
Commented by john santu last updated on 26/Feb/20
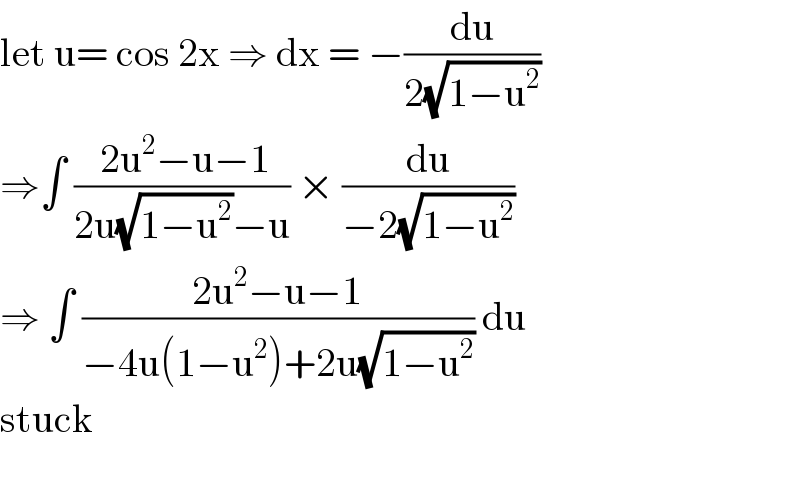
$$\mathrm{let}\:\mathrm{u}=\:\mathrm{cos}\:\mathrm{2x}\:\Rightarrow\:\mathrm{dx}\:=\:−\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\Rightarrow\int\:\frac{\:\mathrm{2u}^{\mathrm{2}} −\mathrm{u}−\mathrm{1}}{\mathrm{2u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }−\mathrm{u}}\:×\:\frac{\mathrm{du}}{−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\int\:\frac{\mathrm{2u}^{\mathrm{2}} −\mathrm{u}−\mathrm{1}}{−\mathrm{4u}\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)+\mathrm{2u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\:\mathrm{du} \\ $$$$\mathrm{stuck} \\ $$$$ \\ $$
Commented by MJS last updated on 26/Feb/20
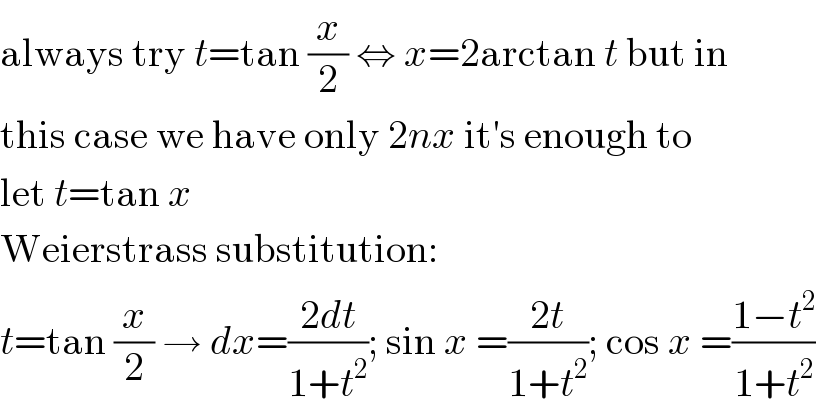
$$\mathrm{always}\:\mathrm{try}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t}\:\mathrm{but}\:\mathrm{in} \\ $$$$\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{have}\:\mathrm{only}\:\mathrm{2}{nx}\:\mathrm{it}'\mathrm{s}\:\mathrm{enough}\:\mathrm{to} \\ $$$$\mathrm{let}\:{t}=\mathrm{tan}\:{x} \\ $$$$\mathrm{Weierstrass}\:\mathrm{substitution}: \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$
Commented by john santu last updated on 26/Feb/20
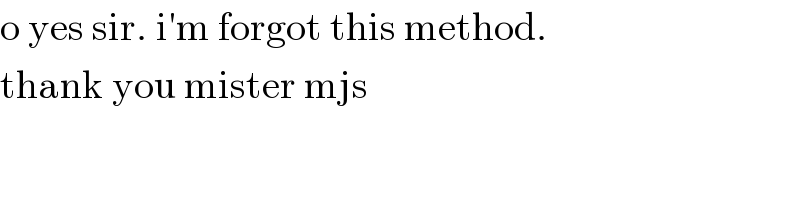
$$\mathrm{o}\:\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}'\mathrm{m}\:\mathrm{forgot}\:\mathrm{this}\:\mathrm{method}. \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mister}\:\mathrm{mjs} \\ $$
Answered by MJS last updated on 26/Feb/20
![∫((cos 4x −cos 2x)/(sin 4x −cos 2x))dx= [t=tan x → dx=(dt/(t^2 +1))] =2∫(((t^2 −3)t^2 )/((t−1)(t+1)(t−2−(√3))(t−2+(√3))(t^2 +1)))dt= =(1/2)∫(dt/(t−1))+(1/6)∫(dt/(t+1))+((1+(√3))/6)∫(dt/(t−2−(√3)))+((1−(√3))/6)∫(dt/(t−2+(√3)))−∫(t/(t^2 +1))dt and all of them are easy to solve](https://www.tinkutara.com/question/Q83007.png)
$$\int\frac{\mathrm{cos}\:\mathrm{4}{x}\:−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{4}{x}\:−\mathrm{cos}\:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{3}\right){t}^{\mathrm{2}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{2}+\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}−\mathrm{2}−\sqrt{\mathrm{3}}}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}−\mathrm{2}+\sqrt{\mathrm{3}}}−\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\mathrm{and}\:\mathrm{all}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
