Question Number 126954 by bramlexs22 last updated on 25/Dec/20
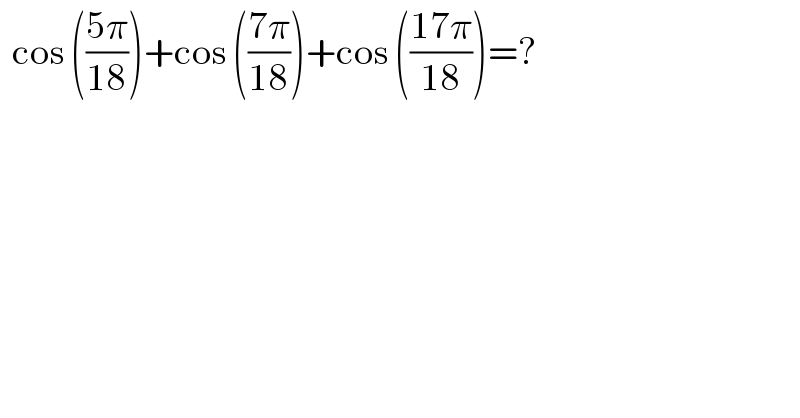
$$\:\:\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{18}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{7}\pi}{\mathrm{18}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{17}\pi}{\mathrm{18}}\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Dec/20
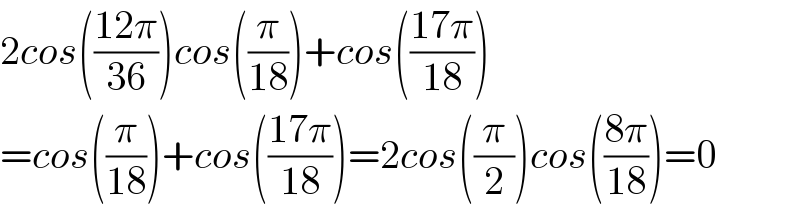
$$\mathrm{2}{cos}\left(\frac{\mathrm{12}\pi}{\mathrm{36}}\right){cos}\left(\frac{\pi}{\mathrm{18}}\right)+{cos}\left(\frac{\mathrm{17}\pi}{\mathrm{18}}\right) \\ $$$$={cos}\left(\frac{\pi}{\mathrm{18}}\right)+{cos}\left(\frac{\mathrm{17}\pi}{\mathrm{18}}\right)=\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{8}\pi}{\mathrm{18}}\right)=\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 25/Dec/20
��
Answered by Olaf last updated on 25/Dec/20
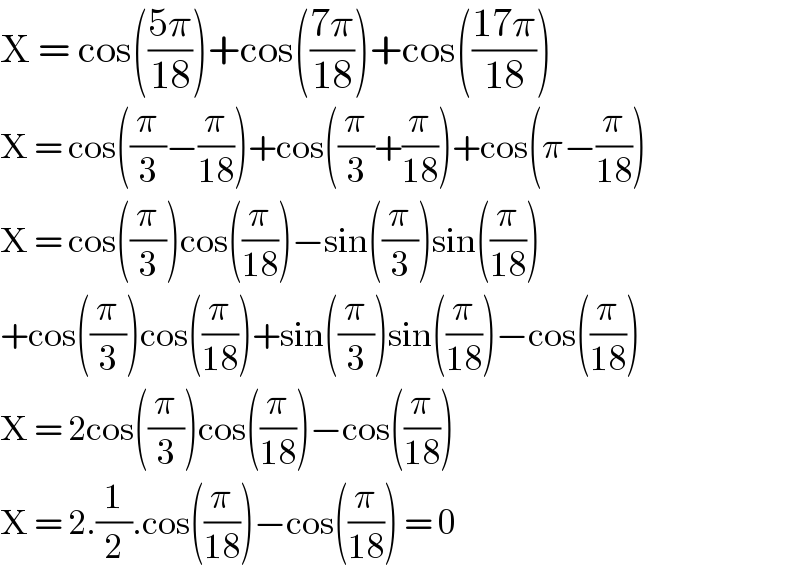
$$\mathrm{X}\:=\:\mathrm{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{18}}\right)+\mathrm{cos}\left(\frac{\mathrm{7}\pi}{\mathrm{18}}\right)+\mathrm{cos}\left(\frac{\mathrm{17}\pi}{\mathrm{18}}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{18}}\right)+\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{18}}\right)+\mathrm{cos}\left(\pi−\frac{\pi}{\mathrm{18}}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right)−\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{18}}\right) \\ $$$$+\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right)+\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{18}}\right)−\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{2cos}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right)−\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right) \\ $$$$\mathrm{X}\:=\:\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right)−\mathrm{cos}\left(\frac{\pi}{\mathrm{18}}\right)\:=\:\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 25/Dec/20
:-)
